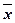Ковариация и корреляция
Различают выборочную и теоретическую ковариацию.
Выборочной ковариацией двух переменных x, y называется средняя величина произведения отклонений этих переменных от своих средних, т.е.
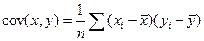, или 
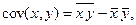
где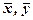 
– выборочные средние переменных x, y.
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
Пусть данные наблюдений переменных x, y представлены в виде точечного графика – диаграммы рассеяния наблюдения, рис. 6.
|
|
Рис. 6
Точка (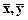 
) на диаграмме является центром рассеяния переменных x, y.
Вертикальная и горизонтальная прямые, проведенные через точку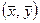 
разделяют диаграмму рассеяния на четыре области.
Наблюдения в областяхI, III, в которых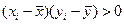 
, дают положительный вклад в ковариацию, а в областях II, IV, в которых 
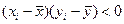– отрицательный вклад.
Если положительные вклады преобладают над отрицательными, то ковариация будет положительной, иначе – отрицательной.
Положительной ковариации отвечает положительная связь, а отрицательной – отрицательная связь.
При положительной (прямой) связи с увеличением одной переменной другая переменная в среднем также увеличивается, и, наоборот, при отрицательной (обратной) связи.
Заметим, что: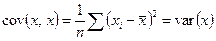 
.
Правила расчета ковариации (a,b – const):
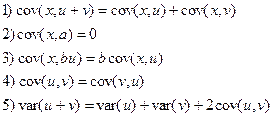
Доказательство вытекает из определения ковариации. Например:
2) 
.
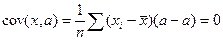5) var(u + v) = cov(u + v, u + v) = cov(u,u) + cov(v,v) + 2cov(u,v) = var(u) + var(v) + 2cov(u,v).
Теоретической ковариацией случайных величин X, Y называется математическое ожидание произведения отклонений этих величин от своих средних значений, т.е.
Cov(X, Y) = M [(X – mX) (Y – mY)], где mX = M(X), mY = M(Y).
Запись Cov(X, Y) указывает на то, что ковариация рассматривается по генеральной совокупности.
Заметим, что Сov(X,X) = M(X–mX)2 =sX2.
Свойство.Если случайные величины X,Y независимы, то теоретическая ковариация равна нулю, т.е. Сov(X,Y) = 0.
Более точной мерой зависимости между величинами является коэффициент корреляции. Различают теоретический и выборочный коэффициенты корреляции.
Теоретический коэффициент корреляции определяется выражением:
,
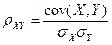где sX, sY – стандартные отклонения случайных величин X, Y.
Коэффициент корреляции является безмерной величиной, изменяющейся в пределах –1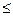 
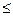r 1.
Коэффициент корреляции показывает степень (тесноту) линейной связи двух случайных величин, причем:
· r > 0 при положительной связи и r = 1 при строгой положительной линейной связи;
· r < 0 при отрицательной связи и r = –1 при строгой отрицательной линейной связи;
· r = 0 при отсутствии линейной связи.
Определение. Случайные величины X, Y называются некоррелированными, если r = 0, и коррелированными, если r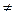 
0.
Независимость случайных величин X, Y означает отсутствие любой связи между ними (линейной и нелинейной), а некоррелированность – отсутствие только линейной связи.
Если случайные величины X, Y независимы, то они некоррелированы (r = 0), но из некоррелированности не следует их независимость, т.е. равенство r = 0 указывает на отсутствие линейной связи между величинами, но не на отсутствие связи между ними вообще.
Выборочный коэффициент корреляции определяется выражением:
.
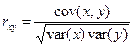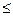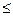При каждом конкретном значении rxy выборочный коэффициент корреляции является случайной величиной, изменяющийся в пределах –1 r 1.
На рис. 7 отражен геометрический смысл коэффициента корреляции.
|
|
|
|
Рис. 7
Если r = 0 для генеральной совокупности, то это необязательно означает, что r = 0 для выборочной совокупности.
Дата добавления: 2016-02-16; просмотров: 4945;