Проверка статистических гипотез

Статистической гипотезой H называется предположение относительно параметра или вида распределения случайной величины.

Нулевой гипотезой H₀ называют выдвигаемую гипотезу. Обычно считают, что H₀ – гипотеза об отсутствии различий.

Конкурирующей гипотезой H₁называют гипотезу, которая противоречит нулевой. Гипотеза H₁ – гипотеза о значимостиразличий.

Проверку статистической гипотезы выполняют на основании результатов выборки. Поскольку выборка производится случайным образом и ограничена, то появляется возможность принятия ошибочного решения.

Статистическим критерием называют случайную величину, которая служит для проверки нулевой гипотезы. В качестве статистического критерия выбирается такая случайная величина, например t, точное или приближенное распределение которой известно.

Наблюдаемым значением t_. называют значение критерия, вычисленное по данным выборки.

Уровнем значимости aназывается вероятность того, что будет отвергнута правильная нулевая гипотеза, т.е. .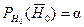

Уровень значимости aустанавливается заранее. Выбор, например 5%-го уровня значимости означает, что в пяти случаях применения критерия из ста верная гипотеза будет отвергнута. Стремление к уменьшению aведет к одновременному уменьшению вероятности отвергнуть гипотезу, когда она является ложной.

В экономических исследованиях проверку гипотез осуществляют при 5%-ном и 1%-ом уровнях значимости, которые называются стандартными уровнями значимости.

Замечание.Между переменнымиt и αустановлено взаимно однозначное соответствие.

Проверку статистических гипотез можно произвести двумя способами.

Способ 1.Стандартным уровням значимости α соответствуют определенные значения t_кр= t(α), называемые критическими точками.

Практически, значения критических точек t_кр.1 для α = 0,05 и t_кр.2 для α = 0,01 определяются по таблицам известного распределения выбранного критерия. Также соответствующие значения можно вычислить с помощью функций Excel.

Для наглядности процесса принятия решения на координатной оси t указывают эти критические точки, рис. 4

Рис. 4

Критические точки разбивают множество значений критерия tна три непересекающиеся области.

Область левее критической точки t_кр.1называется зоной незначимости. Если t <t_кр.1 ,то H₀ принимается на уровне значимости 0,05, и тем более на уровне 0,01.

Область правее критической точки t_кр.2называется зоной значимости. Если t > t_кр.2,тоH₀ отвергается на уровне значимости 0,01, и тем более отвергается на уровне 0,05.

Область между двумя критическими точкаминазывается зоной неопределенности.Если t_кр.1 < t _.< t_кр.2 ,то H₀ отвергается на уровне 0,05, но принимается на уровне 0,01.

Таким образом, если наблюдаемое значение критерия t больше критического значения t_кр для заданного стандартного уровня значимости, то гипотеза H₀ отвергается и исследуемый показатель является статистически значимым.

Способ 2. Наблюдаемому значению критерия t соответствует определенное значение уровня значимости α(t), которое в дальнейшем будем обозначать как значимость t = α (наблюдаемое значение t). Практически, значимость t можно определить с помощью функции Excel.

Для наглядности процесса принятия решения на координатной оси a указывают его стандартные значения 0,01 и 0,05, рис. 5.

Рис.5

Стандартные значения 0,01 и 0,05 разбивают множество значений α на три непересекающиеся области.

Область левее стандартной точки 0,01 является зоной значимости.

Если значимость t < 0,01, то Н₀ отвергается на уровне 0,01, и тем более отвергается на уровне 0,05_.

Область правее стандартной точки 0,05 является зоной незначимости.

Если значимость t > 0,05, то H₀ принимается на уровне 0,05, и тем более принимается на уровне 0,01.

Область между двумя стандартными точкамиявляется зоной неопределенности. Если 0,01 < значимость t _.< 0,05, то H₀ принимается на уровне 0,01, но отвергается на уровне 0,05.

Таким образом, если значимостьtменьше заданного стандартного уровня, то гипотеза H₀ отвергается и исследуемый показатель является статистически значимым.

Такая проверка осуществляется в современных статистических пакетах на компьютере, в которых значимость критерия подсчитывается непосредственно в процессе работы.

Если в качестве критерия проверки нулевой гипотезы используется случайная величина, подчиненная распределению Стьюдента, то ее обозначают через t (t-статистика), а подчиненная распределению Фишера – через F (F-статистика).

t-статистика часто используется для проверки гипотезы о значимости выборочной оценки исследуемого параметра и нахождения интервальных оценок параметра. В качестве критерия t принимается отношение выборочной оценки параметра к ее стандартной ошибке: .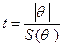

F-статистика используется для проверки гипотезы о равенстве дисперсий. В качестве критерия Fпринимают отношение исправленных выборочных дисперсий: .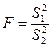

В дальнейшем для проверки статистических гипотез будем использовать в основном способ 2.