Операция суммирования

Пусть величина X задается последовательность данных x₁, x₂,…, x_n, каждое из которых можно записать как x_i, i = 1, …, n.

Сумма этих чисел обозначается:

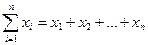, причем .

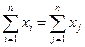Если из контекста ясно, каковы начальный и конечный суммируемые члены, то часто используют сокращенные обозначения:

.

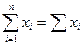Сумма квадратов этих чисел обозначается:

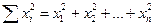
Обозначим средние значения величин X, X², XY соответственно как:

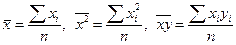
Имеет место неравенство: .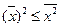

Правила суммирования (a, b – константы):

1.

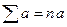
2.

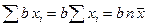
3.

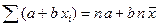
4.

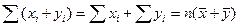
5.

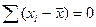
6.

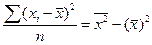
7.

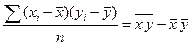
Случайные величины

Случайной величиной (переменной) называется величина, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел.

Случайные величины обозначаются прописными буквами, а их возможные значения – строчными.

Для полной характеристики случайной величины должны быть указаны не только все ее значения, но и их вероятности.

Универсальным способом задания случайной величины Х является задание её функции распределения.

Функцией распределения F(x) случайной величины X называется вероятность того, что величина X принимает значение, меньшее x, т.е.

.

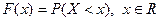Свойства функции распределения:

1)0 ≤ F(x) ≤ 1 при любых x Î R;

2) P(x₁ 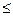X x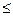₂) = F(x₂) – F(x₁);

3) F(x) – неубывающая функция;

4) .

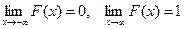Различают дискретные и непрерывные случайные величины.

Дискретной называется случайная величина, которая принимает отдельные, изолированные друг от друга значения. Число возможных значений дискретной случайной величины конечно или счётно.

Дискретную случайную величину удобнее задавать не в виде функции распределения, а рядом распределения.

При табличном задании ряда распределения первая строка таблицы содержит возможные значения случайной величины, а вторая – соответствующие им вероятности, т.е.

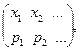гдеp_i = P(X = x_i), Sp_i = 1.

Графическое изображение ряда распределения называется полигоном распределения.

Непрерывнойназывается случайная величина, множество значений которой непрерывно заполняет некоторый числовой промежуток. Число возможных значений непрерывной случайной величины бесконечно.

Задать непрерывную случайную величину рядом распределения невозможно, поэтому её задают функцией распределения F(x).

Вместо функции распределения F(x) для непрерывной случайной величины обычно используется плотность распределения вероятностей f(x).

Плотностью распределения f(x) непрерывной случайной величины называется производная от функции распределения, т.е. f(x) = F¢(x).

Свойства плотности распределения:

1) f(x) 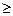0 при любых x Î R

2)

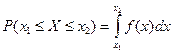
3)

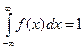
В основе математической статистики лежат понятия генеральной и выборочной совокупностей.

Генеральная совокупность – множество всех значений (исходов) случайной величины, которые она может принять в процессе наблюдения. Например, данные о доходах всех жителей страны.

Выборочная совокупность (выборка) – множество наблюдений, составляющих лишь часть генеральной совокупности.

Для любой случайной величины важную роль, помимо функции распределения, играют числовые характеристики её распределения.