II. Выборочная совокупность

Пусть из генеральной совокупности с распределением F(x) извлекается выборка объема n. Считаем, что выборочные наблюдения X₁, X₂,…, X_n независимы и имеют одинаковые распределения.

Выборочной средней называется среднее арифметическое наблюдаемых значений случайной величины в выборке, т.е.

.

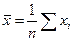Выборочной дисперсией (вариацией) называется среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины в выборке от их среднего значения, т.е.

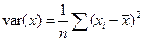, или .

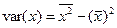Свойства выборочной дисперсии, (a, b – const):

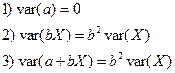
Значения 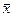,var(X) являются числовыми характеристиками выборочной совокупности.

Для разных выборок, взятых из одной и той же генеральной совокупности, выборочные средние и дисперсии будут различны, т.е. выборочные характеристики являются случайными величинами.

Замечание. Математическое ожидание М(Х) – это операция нахождения средней из выборочных средних гипотетических выборок, покрывающих генеральную совокупность.

Из условия, что выборочные наблюдения X₁, X₂, …, X_n независимы и имеют одинаковые распределения, вытекает, что:

.

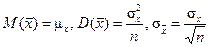Центральная предельная теорема закона больших чисел устанавливает, что распределение средней выборочной 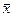при достаточно большом n является нормальным, т.е.

.

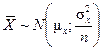Пример. 1.1.Вычислить выборочные характеристикипо исходным данным

Исходные данные (x) и расчетные показатели (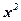 ) представим в виде расчетной таблицы.

№
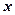
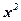
Итого
Среднее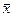

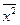
Выборочные характеристики:

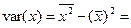132 – 100 =32.

Для вычисления выборочных средней и дисперсии в Excel можно использовать функции: 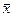= СРЗНАЧ(массив x), var(x) = ДИСПР(массив x).