Генеральная совокупность

Математическим ожиданием дискретной случайной величины называется сумма произведений всех её значений на соответствующие им вероятности, т.е.

,

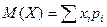где суммирование производится по всем возможным значениям случайной величины.

Математическое ожидание непрерывной случайной величины определяется выражением:

,

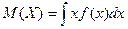где интегрирование производится на всем интервале, в котором определена функция f(x).

Математическое ожидание случайной величины – это среднее ее значение по генеральной совокупности, обозначается .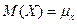

Геометрически математическое ожидание случайной величины – это центрее распределения.

Математическое ожидание функции g(X) определяется выражением:

,

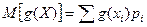где суммирование производится по всем возможным значениям x_i.

В частности, если g(X) = X², то M(X²) = Sx_i² p_i.

Теоретическая (генеральная) дисперсия случайной величины определяется как математическое ожидание квадрата отклонения случайной величины X относительно её средней, т.е.

.

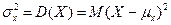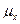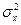Замечание. Если ясно, о какой переменной идет речь, нижний индекс в или может быть опущен.

Для вычисления дисперсии часто используется другое выражение, получаемое из определения дисперсии:

.

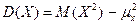Геометрически дисперсия – мера рассеяния случайной величины относительно средней (центра). Размерность дисперсии не совпадает с размерностью случайной величины.

Стандартным отклонением случайной величины X называется корень квадратный из её дисперсии, т.е. .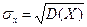

Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности относительно средней (центра).

Определение. Случайные величины X, Y называются независимыми, если P(X = x; Y = y)= P(X = x) P(Y = y) для любых значений x, y.

Следствие.Если случайные величины X,Y независимы, то

M(XY) = M(X)M(Y),

.

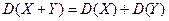Заметим, что M(X) и D(X) – это числовые характеристики генеральной совокупности (числа), а не функции.

Нормальное распределение случайной величины X характеризуется лишь двумя параметрами: средним значением m и дисперсией s².

Это обозначается как X ~ N(m, s²).

График плотности нормального распределения f(x) имеет колоколообразный вид (рис. 1), симметричный относительно центра m. Максимум этой функции находится в точке x = m, а разброс относительно этой точки определяется параметром s. Чем меньше значение s, тем более острый и высокий максимум f(x).

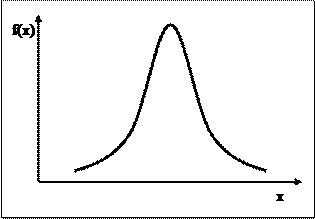
Рис. 1