Проверка гипотезы о корреляции случайных величин

Пусть по данным выборки объема n получен выборочный коэффициент корреляции r ¹ 0. Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции.

Выдвигаются гипотезы:

.

Проверка нулевой гипотезы H₀ используется при установлении статистической значимости выборочного коэффициента корреляции.

В качестве критерия проверки нулевой гипотезы принимается случайная величина

,

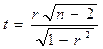которая имеет t-распределение Стьюдента с n = n – 2 степенями свободы. Проверку значимости r произведем двумя способами.

1. Критическое значение t_кр при заданных α и n определяется по таблице t-распределения Стьюдента или в Excel с помощью функции:

t_кр = СТЬЮДРАСПОБР(α; n).

Из сравнения наблюдаемого значенияtс критическим,получаем:

- если t < t_кр , то Н₀ принимается, т.е. r незначим;

- если t > t_кр , то Н₀ отвергается, т.е. r значим.

2. Наблюдаемому (расчетному) значению критерия t соответствует значимость t, которая может быть определена в Excel с помощью функции:

Значимость t = СТЬЮДРАСП(t; n; 2).

Из сравнения значимостиt с заданным стандартным уровнем значимости,получаем:

- если значимость t > стандартного уровня, то r незначим;

- если значимость t <стандартного уровня, то r значим.

Пример 1.2. По исходным данным вычислить ковариацию и коэффициент корреляции между переменными x, yи установить его значимость.

Представим исходные данные и расчетные показатели в виде следующей расчетной таблицы.

№
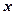
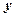
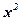
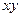
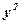
ИТОГО
Среднее				84,8	57,2

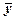
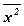
Окончательно имеем:

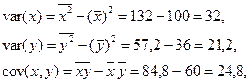
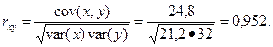
Замечание.В Excel можно по исходным данным получить коэффициент корреляции и его квадрат с помощью функций:

r= ПИРСОН(массив x; массив y), r² = КВПИРСОН(массив x; массив y).

Проверим значимость выборочного коэффициента корреляции.

Наблюдаемое значение критерия:

.

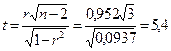Произведем проверку значимости r двумя способами.

1. При α = 0,05 и ν = 3 по таблице или с помощью функции СТЬЮДРАСПОБР(α; n) находим t_кр = 3,18. Поскольку t = 5,4 > t_кр = 3,18, то r = 0,952 значим при 5 % уровне.

2. Наблюдаемому (расчетному) значению критерия t = 5,4 соответствует значимость t = 0,0124, которая может быть определена в Excel с помощью функции СТЬЮДРАСП(t; n; 2). Поскольку значимость t = 0,0124 < 0,05, то коэффициент r = 0,952 значим при 5 % уровне, следовательно, имеется линейная зависимость между переменными.