Алгебраическое представление двоичных чисел в ЭВМ

В ЭВМ могут применяться знаковые и беззнаковые числа.

Для представления чисел со знаком применяют прямые, обратные и дополнительные коды. Код трактуется, как число без знака, а диапазон представляемых чисел разбивается на 2 поддиапазона. Один представляет положительные числа, другой – отрицательные. Принадлежность к поддиапазону указывает значение старшего разряда: 0 – положительный, 1 – отрицательный, то есть старший разряд выступает в качестве знакового, хотя, в общем, код трактуется как число без знака. Обратные и дополнительные коды позволяют заменить неудобные для компьютера и выполняющиеся очень долго, операции вычитания и деления на операцию сложения уменьшаемого с дополнительным кодом вычитаемого. Рассмотрим указанные методы кодирования чисел.

Прямой код числа

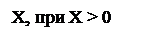
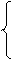Двоичное число Х в прямом коде представлено его абсолютным значением со знаком.

[X]пр =

То есть прямой код положительного числа в закодированном виде совпадает с записью самого числа:

если Х = + 0,X₁X₂ …X_m, ; то [X]_пр = 0,X₁X₂ …X_m.

Прямой код отрицательного числа – Х в закодированном виде имеет вид:

если Х = - 0,X₁X₂ …X_m, то [X]_пр = 1,X₁X₂ …X_m.

Обратный код числа

Обратный код положительного числа совпадает с его прямым кодом:

если Х > 0, то [X]_обр = [X]_{п р} = X

Обратный код отрицательного числа формируется так:

1. в знаковом разряде записывается 1;
2. в цифровых разрядах единицы заменяются нулями, а нули – единицами.

Например, если Х = + 0,101011 = [X]_обр = 0,101011

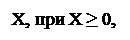
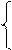Таким образом, формула образования обратного кода дробного двоичного числа Х имеет вид:

[X]_обр =

Для целых чисел при Х < 0, [X]_обр = 2^m-Х, где m – количество разрядов.

Обратный код позволяет операцию вычитания заменить операцией сложения.

Например, Х = + 0,101 и Y = - 0,001 сложить в обратных кодах

[X]обр = 0,101

[Y]обр = 1,110

10,011

Если единица старшего разряда вышла влево, то выполняют операцию циклического переноса, то есть прибавляют единицу к младшему разряду.