Раздел 2 Информационно - логические основы ЭВМ
Тема 2.1 Системы счисления и форматы данных ЭВМ
План лекции
– Системы счисления:
двоичная система счисления;
двоичная арифметика;
шестнадцатеричная система счисления.
– Преобразование чисел из одной системы счисления в другую.
– Алгебраическое представление двоичных чисел в ЭВМ.
– Форматы представления чисел в ЭВМ:
представление чисел в форме с фиксированной точкой;
представление числа в форме с плавающей точкой.
– Типы данных 32 − разрядных ЭВМ:
форматы данных CPU;
форматы данных FPU;
– Диапазоны чисел, обрабатываемые процессорами.
– Кодирование информации в ЭВМ;
– Физическое представление информации в ЭВМ
Основная часть лекции
Системы счисления
Системой счисления называется способ записи и наименования чисел символами, имеющими определенные количественные значения.
Существуют позиционные и непозиционные системы счисления.
В позиционных системах счисления для написания чисел существует определённый набор символов - цифр, и каждую позицию цифры в числе принято оценивать весом – показателем степени основания системы. 
 Основание системы (Р) – это соотношение весов двух соседних цифр в числе; в каждой системе для записи чисел используется столько цифр, каково основание системы.
Основание системы (Р) – это соотношение весов двух соседних цифр в числе; в каждой системе для записи чисел используется столько цифр, каково основание системы.
Например: Возьмём число 111 в десятичной системе счисления где Р = 10. В этом числе цифра 1 принимает значение единицы, десяти и сотни, то есть положение цифры в числе определяет её значение (вес).
Систем счисления существует довольно много –10-я, 2-я, 8-я, 16-я, и т.д. Некоторые из них приведены в таблице 2.
Таблица 2.1– Распространенные системы счисления
| Системы счисления | Основание системы | Цифры системы счисления |
| Двоичная | Р = 2 | 0, 1 |
| Пятеричная | Р = 5 | 0, 1, 2, 3, 4 |
| Восьмеричная | Р = 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Десятичная | Р = 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Шестнадцатеричная | Р = 16 | 0, 1, 2, 3 ÷ 9, A, B, C, D, E, F |
Если обозначить: а1,а2, … аn – цифры целой части числа;
в1, в2, … вn – цифры дробной части числа;
Р – основание системы счисления.
То любое число Х, в любой системе счисления можно записать в соответствии со следующим уравнением:
Х = аn 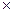 Pn-1 + аn-1
Pn-1 + аn-1 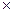 P n-2 + …+ а2
P n-2 + …+ а2 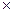 P1 + а1
P1 + а1 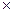 P0, в1
P0, в1 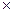 P-1 + в2
P-1 + в2 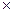 P-2 +
P-2 +
… + вn-1 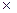 P-n-1 + вn
P-n-1 + вn 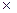 P-n
P-n
Если взять вещественное десятичное число 6321,564, то в соответствии с уравнением его можно представить следующим образом:
6 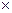 103 + 3
103 + 3 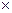 102 + 2
102 + 2 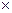 101 + 1
101 + 1 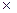 100, 5
100, 5 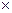 10-1+ 6
10-1+ 6 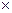 10-2 + 4
10-2 + 4 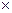 10-3 = 6312,564.
10-3 = 6312,564.
Двоичное число 110101101 в соответствии с формулой можно записать следующим образом:
110101101=1×28+1×27+0×26+1×25+0×24+1×23+1×22+0×21+1×20= 256+128+0+32+0+8+4+0+1 = 429
Дата добавления: 2016-02-24; просмотров: 968;
