Алгоритм перевода чисел из одной системы счисления в другую
1. Из десятичной системы счисления:
o разделить число на основание переводимой системы счисления;
o найти остаток от деления целой части числа;
o записать все остатки от деления в обратном порядке;
2. Из двоичной системы счисления
o Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;
o Для перевода числа в восьмеричную необходимо разбить число на триады.
Например, 1000110 = 1 000 110 = 1068
o Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616
Таблицы для перевода:
| Двоичная СС | Шестнадцатеричная СС |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
| Двоичная СС | Восьмеричная СС |
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
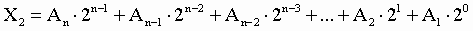
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | |||||||||||
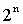
|
Пример .Число 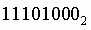 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
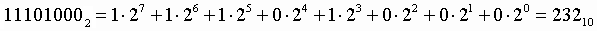
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
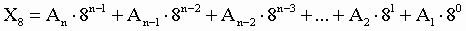
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
| n (степень) | |||||||
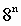
|
Пример .Число 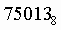 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
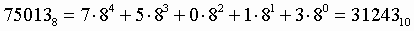
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
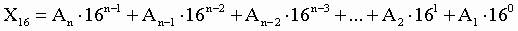
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
| n (степень) | |||||||
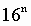
|
Пример .Число 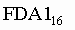 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
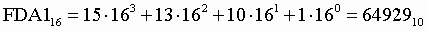
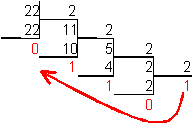
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример.Число 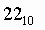 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
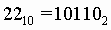
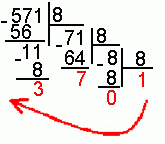
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число 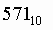 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
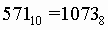
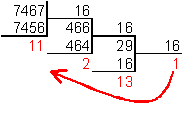
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число  перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число  перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
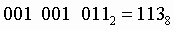
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число 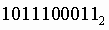 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.
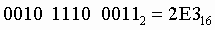
Дата добавления: 2016-03-22; просмотров: 13710;
