Теорема Котельникова

В области цифровой обработки сигналов, Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона, или теорема отсчётов) связывает аналоговые и дискретные сигналы и гласит, что, если аналоговый сигнал 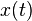имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своимотсчётам, взятым с частотой, большей или равной удвоенной верхней частоте :

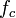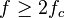
Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Если сигнал имеет разрывы любого рода в функции зависимости его от времени, то его спектральная мощность нигде не обращается в нуль. Именно это подразумевает понятие «спектр, ограниченный сверху конечной частотой ».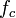

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временно́й характеристике. Соответственно, ширина их спектра бесконечна. В таком случае полное восстановление сигнала невозможно, и, из теоремы Котельникова, вытекают два следствия:

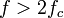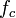1. Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой , где — максимальная частота, которой ограничен спектр реального сигнала;

2. Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал 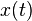можно представить в виде интерполяционного ряда:

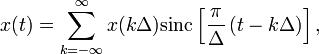
где 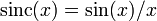— функция sinc. Интервал дискретизации

удовлетворяет ограничениям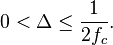

Мгновенные значения данного ряда есть дискретные отсчёты сигнала .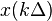

Хотя в западной литературе теорема часто называется теоремой Найквиста со ссылкой на работу 1928 года «Certain topics in telegraph transmission theory», в этой работе речь идёт лишь о требуемой полосе линии связи для передачи импульсного сигнала (частота следования должна быть меньше удвоенной полосы). Таким образом, в контексте теоремы отсчётов справедливо говорить лишь о частоте Найквиста. Примерно в это же время Карл Купфмюллер получил тот же результат^[1]. О возможности полной реконструкции исходного сигнала по дискретным отсчётам в этих работах речь не идёт. Теорема была предложена и доказана В. А. Котельниковым в 1933 году в работе «О пропускной способности эфира и проволоки в электросвязи», в которой, в частности, была сформулирована одна из теорем следующим образом^[2][3]: «Любую функцию 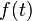, состоящую из частот от 0 до 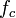, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через 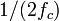секунд». Независимо от него эту теорему в 1949 (через 16 лет) году доказал Клод Шеннон^[4], поэтому в западной литературе эту теорему часто называют теоремой Шеннона.

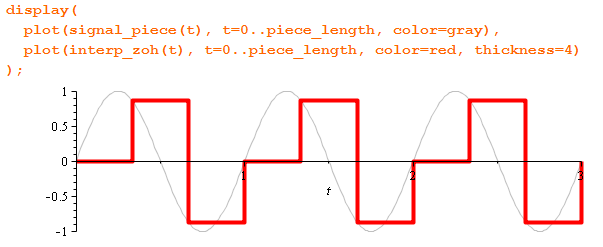
Частота дискретизации (или частота сэмплирования) - частота, с которой происходит оцифровка, хранение, обработка или конвертация сигнала из аналога в цифру. Частота дискретизации, согласно Теореме Котельникова, ограничивает максимальную частоту оцифрованного сигнала до половины своей величины.

Чем выше частота дискретизации, тем более качественной будет оцифровка. Как следует из теоремы Котельникова для того чтобы одназначно восстановить исходный сигнал, частота дискретизации должна превышать наибольшую необходимую частоту сигнала в два раза.

На данный момент, в звуковой технике среднего уровня глубина дискретизации находится в пределах 10-12 бит. Но на слух заметить разницу между 10 и 12 битами не представляется возможным в связи с тем, что человеческое ухо не способно различить такие малые отклонения. Ещё одной причиной бесполезности служит Коэффициент нелинейных искажений УМЗЧ и других компонентов звукогого тракта, явно превышающий величину шага квантования. Бо́льшее разрешение зачастую носит лишь маркетинговый смысл и фактически на слух не заметно.

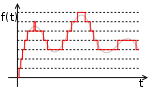
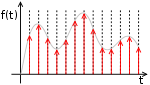
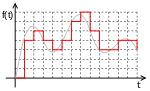
Оцифро́вка (англ. digitization) — описание объекта, изображения или аудио- видеосигнала (в аналоговом виде) в виде набора дискретных цифровых замеров (выборок) этого сигнала/объекта, при помощи той или иной аппаратуры, т. е. перевод его вцифровой вид, пригодный для записи на электронные носители.

Для оцифровки объект подвергается дискретизации (в одном или нескольких измерениях, например, в одном измерении для звука, в двух для растрового изображения) и аналогово-цифровому преобразованию конечных уровней.

Полученный в результате оцифровки массив данных («цифровое представление» оригинального объекта) может использоваться компьютером для дальнейшей обработки, передачи по цифровым каналам, сохранению на цифровой носитель. Перед передачей или сохранением цифровое представление, как правило, подвергается фильтрации и кодированию для уменьшения объема.

Иногда термин «оцифровка» используется в переносном смысле, в качестве замены для соответствующего термина^{[уточнить]}, при переводе информации из аналогового вида в цифровой. Например:

· Оцифровка звука.

· Оцифровка видео.

· Оцифровка изображения.

· Оцифровка книг — как сканирование, так и (в дальнейшем) распознавание.

· Оцифровка бумажных карт местности — означает сканирование и, как правило, последующую векторизацию (растрово-векторное преобразование, т. е. перевод в формат векторного описания).

Дискретизация