Оценка ошибки, возникающей при аппроксимации произвольного сигнала рядом Котельникова.

Если — произвольный сигнал, то его можно представить суммой к в которую входит сигнал со спектром, ограниченным значением а также сигнал ошибки аппроксимации со спектром, занимающим в обшем случае бесконечную полосу частот .

Спектры указанных сигналов не перекрываются, поэтому сигналы ортогональны, а их энергии, т. е. квадраты норм, складываются:

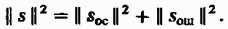
В качестве меры ошибки аппроксимации можно принять расстояние, равное норме сигнала ошибки. Если — энергетический спектр сигнала то по теореме Рэлея

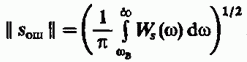
5.3. Дан экспоненциальный видеоимпульс , характеризующийся энергетическим спектром и нормой

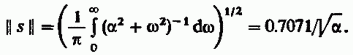
Эффективная длительность этого импульса (см. гл. 2)

Спектр рассматриваемого сигнала неограничен. Поэтому следует предварительно подвергнуть сигнал низкочастотной фильтрации, пропустив его через фильтр нижних частот (ФНЧ). Значение верхней частоты полосы пропускания фильтра следует выбирать в зависимости от того, сколь часто берутся отсчеты сигнала на выходе ФНЧ. Предположим, что за время измеряются отсчетов с интервалом . Согласно теореме Котельникова, это означает, что .

Сигнал с выхода ФНЧ восстанавливается по своим отсчетным значениям точно. Однако по отношению к исходному видеоимпульсу неизбежна ошибка. В данном случае норма сигнала ошибки

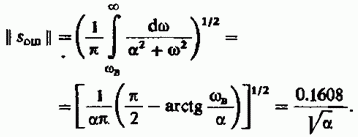
Относительная ошибка аппроксимации