Интегральная теорема Лапласа. Найдем вероятность того, что событие наступит в испытаниях не менее раз и не более раз.

Найдем вероятность того, что событие 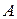наступит в 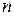испытаниях 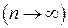не менее 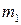раз и не более 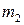раз.

Интегральная теорема Лапласа. Если вероятность наступления события 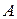в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие 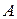наступит в 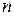испытаниях от 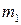до 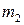раз, приближенно равна определенному интегралу

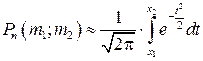, где , .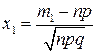

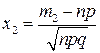Обозначим интеграл 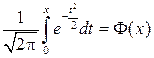, функция 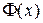называется функцией Лапласа и имеет следующие свойства.

1. Функция Лапласа – нечётная, .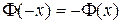

2. , .

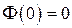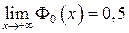3. 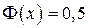при .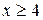

Функция Лапласа табулирована (приложение 2), причём в силу свойств 1 и 3 таблицу её значений достаточно иметь на промежутке [0;4].

С использованием функции Лапласа интегральная теорема Лапласа примет вид: 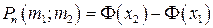, где .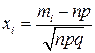

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажутся непроверенных от 70 до 100 деталей.

Решение. Производится 400 независимых испытаний, вероятность «успеха» в каждом 0,2. По условию , , , , .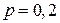

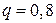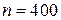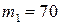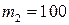Тогда , .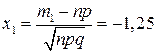

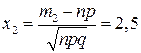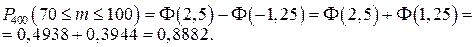
Значения 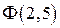и 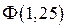найдены по таблице приложения 2.

Случайные величины

Дискретной случайной величиной (ДСВ) называют случайную величину (СВ), возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями.

Число возможных значений ДСВ может быть конечным или бесконечным.

Но распределения случайных величин далеко не исчерпываются дискретными распределениями. Так, например, если точка бросается наудачу на отрезок [0,1], то можно задать случайную величину, равную координате этой точки. Но число значений этой случайной величины бесконечно, так что ее распределение дискретным не является. Да и вероятность этой случайной величине принять каждое из своих возможных значений (попасть в точку) равна нулю. Поэтому:

случайную величину, возможные значения которой принадлежат некоторому промежутку, называют непрерывной случайной величиной.