Геометрическое распределение. Говорят, что случайная величина имеет геометрическое распределение с параметром , где , если принимает значения с вероятностями
Говорят, что случайная величина 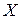 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 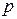 , где
, где 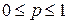 , если
, если 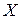 принимает значения
принимает значения  с вероятностями
с вероятностями 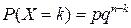 , где
, где  . Случайная величина
. Случайная величина 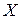 с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха
с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха 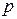 .
.
Таблица распределения СВ 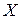 имеет вид:
имеет вид:
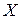
| k | … | |||

| 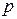
| 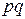
| 
| 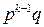
| … |
Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством «нестарения». Пусть величина 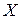 обозначает, скажем, время безотказной работы (измеряемое целым числом часов) некоторого устройства. Предположим, что для величины
обозначает, скажем, время безотказной работы (измеряемое целым числом часов) некоторого устройства. Предположим, что для величины 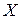 вероятность принять любое свое значение
вероятность принять любое свое значение 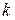 равна
равна 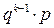 . Справедливо следующее утверждение:
. Справедливо следующее утверждение:
пусть 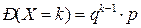 . Тогда для произвольных
. Тогда для произвольных 
 .
.
Данному равенству можно придать следующее звучание: если известно, что устройство проработало без отказов n часов, то вероятность ему работать еще не менее k часов точно такая же, как вероятность проработать не менее k часов для нового устройства.
Можно прочесть эту формулу и так: вероятность работающему устройству проработать еще сколько-то часов не зависит от того момента, когда мы начали отсчет времени, или от того, сколько уже работает устройство.
Дата добавления: 2016-04-22; просмотров: 612;
