Математическое ожидание

«Случайных величин без мат. ожидания не бывает, так как, если у нас есть случайная величина, мы всегда в праве от нее что-нибудь ожидать».

Из студенческой контрольной работы.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

.

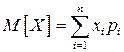Замечание. Если число возможных значений СВ бесконечно, то математическое ожидание равно сумме ряда, если этот ряд сходится абсолютно:

.

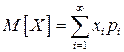Пример.Распределение ДСВ задано рядом распределения

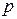
	0,3	0,5	0,2

Математическое ожидание .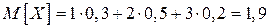

Математическое ожидание случайной величины есть ЧИСЛО!

Математическое ожидание приближенно равно среднему значению СВ, с тем большей точностью, чем больше число измерений. Поэтому математическое ожидание называют часто просто средним значением случайной величины.

Отметим, что математическое ожидание случайной величины всегда определяется однозначно и уже не является величиной случайной.

Математическим ожиданием 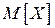непрерывной случайной величины 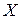, распределенной на промежутке 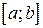с плотностью распределения 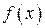называется определенный интеграл от произведения плотности СВ на :

.

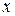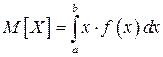Если же непрерывная случайная величина 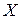распределена на промежутке 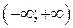, то .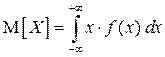

Если же 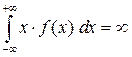, то говорят, что математическое ожидание не существует.

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой величине: .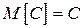

2. Постоянную 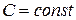можно вынести за знак математического ожидания: .

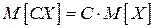3. Математическое ожидание суммы двух СВ 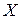и 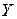равно сумме математических ожиданий этих величин: .

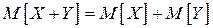4. Математическое ожидание произведения двух независимых СВ равно произведению математических ожиданий этих величин: .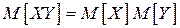

Пример.Найти математическое ожидание непрерывной случайной величины, если известна плотность распределения: .

Решение. По определению получаем:

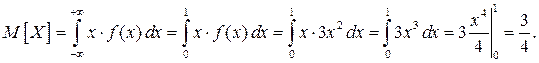
Пример. Найти математическое ожидание случайной величины 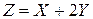, если известны математические ожидания 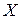и : .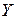

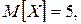
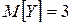Решение. Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно выносить за знак математического ожидания), получим:

.

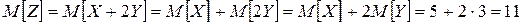Мода и медиана СВ

Числовыми характеристиками, характеризующими положение многоугольника распределения или кривой распределения, являются мода и медиана СВ.

Модой 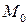дискретной СВ называется наиболее вероятное значение случайной величины.

Модой 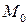непрерывной СВ называется такое значение СВ, при котором плотность ее распределения максимальна.

Многоугольник распределения и кривая распределения могут иметь несколько максимумов или не иметь их вообще. В последнем случае говорят, что моды не существует.

Медианой 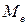СВ называется такое ее значение, для которого одинаково вероятно, окажется случайная величина больше или меньше 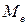, то есть .

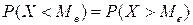Геометрический смысл. Медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делиться пополам.

Значение функции распределения в медиане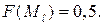

Замечание. Если распределение одномодально и симметрично, то математическое ожидание, мода и медиана совпадают.