Равномерное распределение
Говорят, что случайная величина 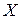 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 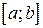 , если ее плотность распределения имеет вид:
, если ее плотность распределения имеет вид:
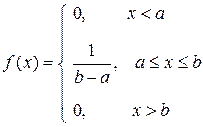 .
.
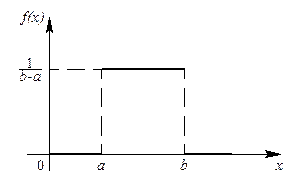
|
| Рис. 5. Кривая равномерного распределения |
Функция распределения имеет вид:
 .
.
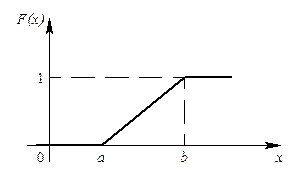
|
| Рис. 6. График функции равномерного распределения |
Например, равномерное распределение присутствует при взвешивании на весах – ошибка взвешивания равномерно распределена в интервале  .
.
Пример.Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, не превышающая 0,02 А.
Решение.Ошибку округления можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями.
Плотность равномерного распределения 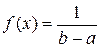 , где
, где 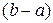 – длина интервала, в котором заключены возможные значения Х, вне этого интервала
– длина интервала, в котором заключены возможные значения Х, вне этого интервала 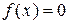 . В данном случае длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому
. В данном случае длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому 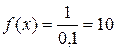 , и
, и
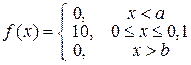 .
.
Ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08).
По формуле 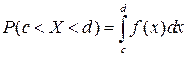 получим:
получим:
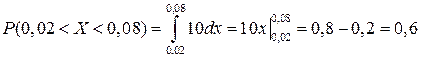 .
.
Дата добавления: 2016-04-22; просмотров: 812;
