Непрерывные случайные величины
Расстояние, которое пролетит пуля после выстрела – величина случайная, однако она не является дискретной, т.к. нельзя полностью перечислить все возможные её значения, а можно лишь указать интервал, которому принадлежат все возможные значения. Поэтому можно назвать случайную величину непрерывной, если возможные её значения принадлежат некоторому промежутку.
Очевидно, что для непрерывной СВ не существует ряда распределения, так как нельзя перечислить все возможные значения случайной величины.
Случайная величина 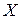 имеет так называемое абсолютно непрерывное распределение, если существует неотрицательная функция
имеет так называемое абсолютно непрерывное распределение, если существует неотрицательная функция 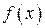 такая, что для любого
такая, что для любого 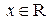 функцию распределения
функцию распределения 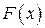 можно представить в виде:
можно представить в виде:
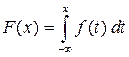 .
.
При этом функция 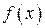 называется плотностью распределения вероятностей случайной величины
называется плотностью распределения вероятностей случайной величины 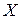 .
.
График плотности распределения называется кривой распределения.
Плотность распределения обладает свойствами:
1. 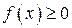 для любого значения
для любого значения 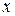 ;
;
2. 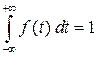 – полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
– полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
3. Вероятность попадания случайной величины на заданный интервал 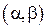 равна:
равна:
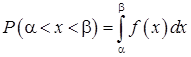 .
.
4. Связь между функцией распределения и плотностью непрерывной случайной величины:
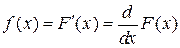 и
и
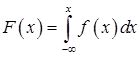 .
.
Итак, значение плотности распределения в точке 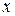 равно вероятности «попадания» непрерывной случайной величины
равно вероятности «попадания» непрерывной случайной величины 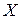 в малый промежуток
в малый промежуток 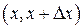 . Т.е. плотность распределения показывает, насколько плотно (в смысле вероятности) сгруппированы возможные значения непрерывной случайной величины вблизи точки
. Т.е. плотность распределения показывает, насколько плотно (в смысле вероятности) сгруппированы возможные значения непрерывной случайной величины вблизи точки 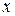 .
.
Пример.Случайная величина 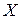 задана функцией распределения
задана функцией распределения
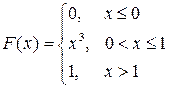 .
.
Найти плотность распределения 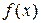 , построить графики функций
, построить графики функций 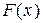 и
и 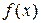 .
.
Решение.Используя свойство 4, находим:
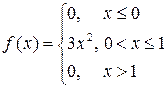 .
.
Графики функций 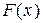 и
и 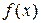 изображены на рис. 3 и рис. 4.
изображены на рис. 3 и рис. 4.
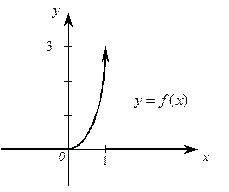
Рис. 3. Кривая распределения
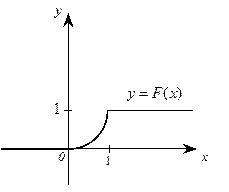
Рис. 4. График функции распределения
Пример.Для случайной величины 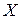 известна плотность распределения:
известна плотность распределения:
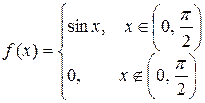 .
.
Требуется найти функцию распределения 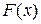 .
.
Решение. Будем использовать свойство 4 плотности распределения.
Рассмотрим следующие промежутки:
Пусть 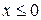 , тогда
, тогда 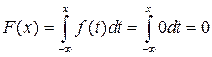 ;
;
Пусть 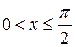 , тогда
, тогда
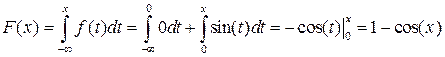 ;
;
Пусть 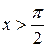 , тогда
, тогда 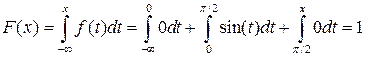 .
.
Окончательно получим:
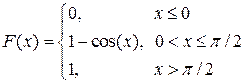 .
.
Дата добавления: 2016-04-22; просмотров: 706;
