Векторные и скалярные величины в теории электромагнитного поля

Величины, значения которых могут быть изображены положительными или отрицательными числами (скалярами),называются скалярными. Величины, значения которых характеризуются (в отличие от скаляра) не только количеством, но и направлением в пространстве называются векторнымии могут быть изображены векторами. 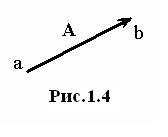Вектор – отрезок (рис.1.4), имеющий определенную длину и направление (обозначается 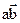или A,иногда 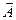. a – начало, b – конец вектора ). Длина вектора A (модуль или абсолютная величина) обозначается A или |А|. Два вектора считаются равными, если равны их модули, совпадают их направления.

В произвольной ортогональной системе координат запись вектора имеет следующий вид

A = I₁A₁ + I₂A₂ + I₃A₃.

Проекции A₁.A₂ и A₃ называются компонентами или составляющими вектора A; I₁, I₂ и I₃ – единичные векторы или орты в выбранной системе координат.

В декартовой системе координат

A = x₀A_x +y₀A_y + z₀A_z ,

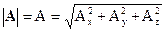
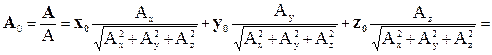
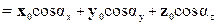
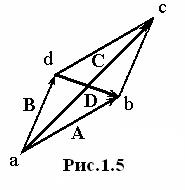С у м м а двух векторов Aи B– диагональ ac (вектор С)параллелограмма построенного на этих векторах (рис.1.5). Разностью A–B называется сумма векторов A и(–B) (диагональ db параллелограмма на рис.1.5).

Сложение (вычитание) в векторной алгебре означает алгебраическое сложение (вычитание) компонент векторов:

A ± B = l₁(A₁ ± B₁) + l₂(A₂ ± B₂) + l₃(A₃ ± B₃)

Где l₁, l₂ и l₃ орты системы координат

Умножение векторов

Скалярное умножение векторов. Скалярным произведением векторов A и B называют скаляр, равный произведению длин этих векторов на косинус образованного ими угла j. Скалярное произведение обозначают A^.B или (A,B).

В декартовой системе координат:

(A,B) =A_xB_x + A_yB_y + A_zB_z

Зная скалярное произведение двух векторов, легко найти угол между ними

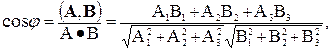
а также величину проекции одного вектора на направление, определяемое другим вектором, например, проекция вектора А на В равна

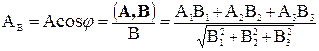
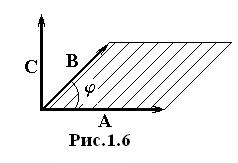Векторное умножение векторов. Векторным произведением векторов A и B называют вектор C модуль, которого равен площади параллелограмма S, построенного на этих векторах, а направление перпендикулярно плоскости этого параллелограмма и определяется правилом буравчика (правилом правого винта) при повороте от первого вектора ко второму по кратчайшему пути (рис. 1.6). Векторное произведение принято обозначать одним из следующих способов:

A´B, [A,B], [AB],

Из определения векторного произведения следует, что

|[A,B]| = AB sin j = S

[A,B] = [l₁A₁ + l₂A₂ + l₃A₃, l₁B₁ + l₂B₂ + l₃B₃] =

=l₁(A₂B₃ – B₂A₃) + l₂(A₃B₁ – B₃A₁) + l₃(A₁B₂ – B₁A₂) .

Или

.

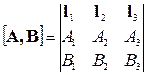[A,B] = - [B,A]

Смешанное произведение трех векторов.

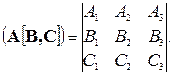
В декартовой системе координат выражение смешанного произведения принимает вид:

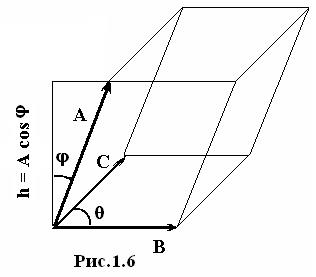
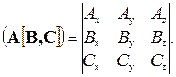
Векторное произведение [B,C] представляет собой вектор, перпендикулярный В и С, модуль которого равен площади параллелограмма, построенного на векторах В и С, т.е. S = │[B,C]│ =BC sin θ (рис.1.6). Этот параллелограмм можно рассматривать как основание параллелепипеда, построенного на векторах А, В и С, следовательно модуль смешанного произведения будет равен произведению площади основания параллелепипеда на его высоту (проекция ребра А на его перпендикуляр к основанию). То есть модуль смешанного произведения равен объему параллелепипеда V, построенному на векторах А, В, и С (рис.1.6).

V=│(A,[B,C])│=│Acosφ│[B,C]││=hS

Нетрудно показать, что смешанное произведение обладает следующим свойством

(А,[B,C]) = (C,[А,B]) = (B,[C,А]) ,

т.е. при циклической перестановке входящих в него векторов ( замене А на В, В на С и С на А) величина смешанного произведения не изменяется.

Двойное векторное произведение. A´(B´C) – вектор, компланарный B и C и может быть вычислен по формуле

A´(B´C) = B(A,C) – C(A,B) .

Л Е К Ц И Я - 2

Ч а с т ь - 2