Классификация векторных полей

Потенциальные поля.

Определенное в области D векторное поле 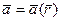называют потенциальным, если существует скалярная функция 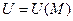такая, что

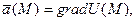
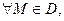
Свойства потенциальных полей

1. Циркуляция потенциального поля 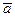по любому замкнутому контуру 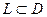равна нулю.

,

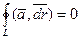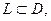
2. ,

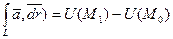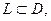
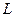- кривая, соединяющая точки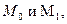

3. Необходимым и достаточным условием потенциальности является

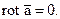
Соленоидальные поля.

Определенное в области D векторное поле 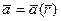называют соленоидальным или трубчатым, если существует вектор – функция 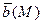, такая что

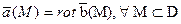
Функцию 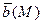при этом называют векторным потенциалом поля.

Если поле 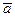соленоидальное и его векторный потенциал равен 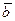, то

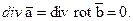
Свойства соленоидальных полей

1. Поток соленоидального векторного поля 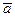через любую замкнутую поверхность 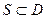равен нулю

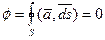
1. Необходимым и достаточным условием соленоидальности является

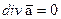
Гармонические поля.

Заданное в области D векторное поле 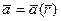называют гармоническим или лапласовым, если оно одновременно и потенциальное и соленоидальное

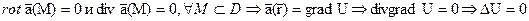
В декартовой системе координат

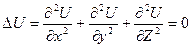- это уравнение Лапласа

и его решение – гармонические функции.

Ч А С Т Ь - 3