Ротор. Теорема Стокса

По определению rot F есть вектор, проекция которого на произвольное направление n выражается следующим образом:

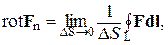
где ΔS – площадка, выбранная так, что n – это нормаль к этой площадке, образующая правовинтовую систему с направлением обхода контура L (если смотреть вдоль вектора n, обход контура L производится по часовой стрелке).

Общая формула для вычисления rot F в криволинейных ортогональных координатах имеет вид:

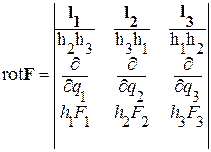
Ротор в декартовой системе координат:

,

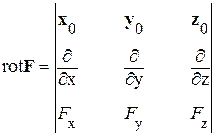или

.

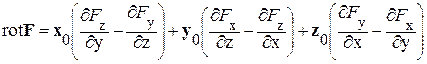В цилиндрической системе координат:

.

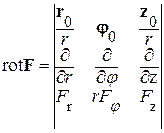В сферической системе координат:

.

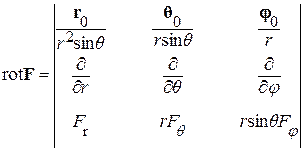Свойства ротора:

1) rot(F+A) = rot F + rot A,

2) rot (mF) = m rot F,

3) rot(yF) = y rot F + [grady, F],

где y – скалярная функция координат.

4) rot grad ψ ≡ 0.

Потенциальные поля (F = grad ψ) являются обязательно «безвихревыми».

5) div rot F ≡ 0

Расходимость вихревого поля равна нулю, т.е. вихревое поле соленоидально.

Теорема Стокса.

,

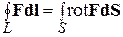связывает между собой циркуляцию вектора по одновитковому замкнутому контуру L с потоком ротора того же вектора через произвольную поверхность S, опирающуюся на этот контур.