Оператор Гамильтона и оператор Лапласа.

Оператор Гамильтона (вектор набла) в декартовой системе координат представляет собой оператор вида

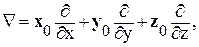
который можно рассматривать как своеобразный вектор. Этот оператор можно применять как к скалярным, так и к векторным функциям.

.

.

.

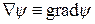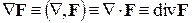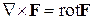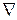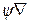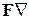При формальном применении оператора как вектора следует помнить, что нет смысла помещать его справа от рассматриваемой функции (например, произведения или , если они используются как окончательные самостоятельные выражения, в векторном анализе не имеют смысла).

Оператор 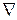удобен и при раскрытии более сложных операций. Например:

.

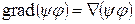1) ,

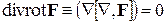так как смешанное произведение трех векторов, из которых два одинаковы, всегда равно нулю.

2)

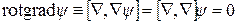
так как векторное произведение одинаково направленных векторов равно 0.

3)

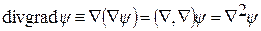
Оператор 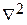(его еще называют оператором Лапласа) в декартовой системе координат имеет вид

.

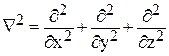Формула получается в результате вычисления скалярного произведения вектора 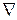на себя самого. Часто оператор 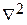обозначают символом Δ.

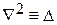
4) .

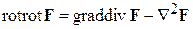Оператор Лапласа в криволинейной ортогональной системе координат определяется как

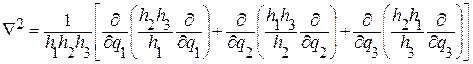
Лапласиан в цилиндрической системе координат

.

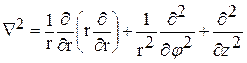Лапласиан в сферической системе координат

.

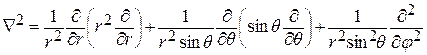В криволинейной ортогональной системе координат оператор Гамильтона имеет вид: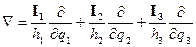

Оператор Гамильтона в цилиндрической системе координат

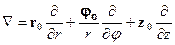
Оператор Гамильтона в сферической системе координат

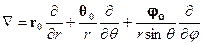
Л Е К Ц И Я - 3