Скалярное поле. Градиент

Скалярное поле. Если в каждой точке некоторой области пространства заданы значения скалярной функции y(r), говорят, что в этой области задано скалярное поле y(r) (поле функции y(r)). Важной характеристикой скалярного поля являются так называемые поверхности уровня (или изоповерхности), на которых y(r) = const.

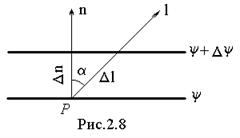Градиент. Рассмотрим две достаточно близкие поверхности уровня и выделим малую область поля, в которой участки этих поверхностей с нужной степенью точности не отличаются от параллельных плоскостей. Пусть разность значений функции y(r), принимаемых ею на выделенных поверхностях уровня, равна Dy. На рис.2.8, где следы этих поверхностей показаны в виде двух прямых, построены также два направления: нормаль n к поверхностям и некоторое произвольное направление l. Поскольку расстояние между плоскостями по нормали – кратчайшее и Dn = Dl cosa, то очевидно

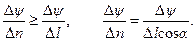
Переходя к пределу при Dn ® 0 получаем (для дифференцируемой y):

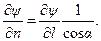
и, следовательно, среди производных функции по всевозможным направлениям, производная по нормали к поверхности уровня является максимальной. Вектор, направленный в сторону наибольшего изменения y и равный по абсолютному значению его скорости, называется градиентом и обозначается grad y .

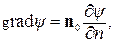
где n₀ – единичный вектор нормали n.

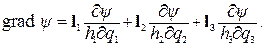
Градиент обладает следующими свойствами

grad (y + j) = grad y + grad j ,

grad (y ^.j) = j grad y + y grad j ,

grad (y / j) = (j grad y –y grad j)/j²,

.

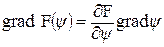С учетом метрических коэффициентов и соответствующих ортов (см. таблицу1) выражение для градиента в декартовой системе координат:

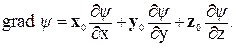
В цилиндрической системе координат:

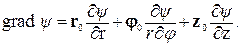
В сферической системе координат:

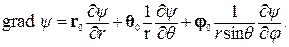
Рассмотрим проекцию grad ψ на произвольно выбранное направление I, обозначаемую grad_Iψ. По определению проекции

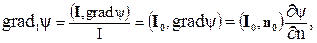
где I₀ – единичный вектор вдоль I, а поскольку (I₀,n₀)=cosα

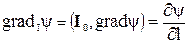
производная скалярной функции по направлению вектора I.