Метод градиентного спуска с постоянным шагом

Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:

.

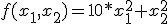Начальное приближение - точка (10,10). Использован критерий останова: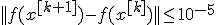

Результаты эксперимента отражены в таблице:

Значение шага	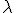Достигнутая точность	Количество итераций
0.1	метод расходится
0.01	2e-4
0.001	2e-3
0.0001	1e-2

Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.

Градиентный метод с дроблением шага

Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:

.

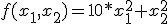Начальное приближение - точка (10,10). Использован критерий останова: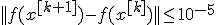

Результаты эксперимента отражены в таблице:

Значение параметра	Значение параметра	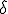Значение параметра	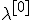Достигнутая точность	Количество итераций
0.95	0.95		5e-4
0.1	0.95		1e-5
0.1	0.1		2e-4
0.1	0.95	0.01	2e-4

Из полученных результатов можно сделать вывод об оптимальном выборе параметров: 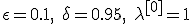, хотя метод не сильно чувствителен к выбору параметров.