Криволинейная ортогональная система координат
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Московский технический университет связи и информатики
_____________________________________________________________
Корнюхин В.И
М О Т э М П
( конспект лекций )
Л Е К Ц И Я - 1
Часть 1
Системы координат
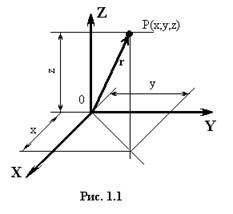 1.1.1Декартова система координат позволяет связать с каждой точкой P пространства три действительных числа (декартовы координаты)- x (абсцисса), y (ордината), z (аппликата), при этом пишут P(x, y, z). Три взаимно перпендикулярные оси X, Y, Z, проходящие через некоторую точку 0, образуют прямоугольнуюили ортогональную систему координат.. Каждая точка P(x,y,z) имеет свой радиус-вектор r (рис.1.1), который в прямоугольной декартовой системе координат может быть представлен в виде:
1.1.1Декартова система координат позволяет связать с каждой точкой P пространства три действительных числа (декартовы координаты)- x (абсцисса), y (ордината), z (аппликата), при этом пишут P(x, y, z). Три взаимно перпендикулярные оси X, Y, Z, проходящие через некоторую точку 0, образуют прямоугольнуюили ортогональную систему координат.. Каждая точка P(x,y,z) имеет свой радиус-вектор r (рис.1.1), который в прямоугольной декартовой системе координат может быть представлен в виде:
r = x0x + y0y + z0z
где: x0,y0,z0 – единичные векторы или орты прямоугольной системы координат.
Длина радиус-вектора r (его численное значение или модуль) обозначается как |r| = r = 0P и является функцией
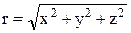
Единичный вектор или орт радиуса вектора r0, направление которого совпадает с направлением r, может быть представлен в виде:
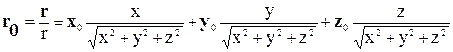
, где
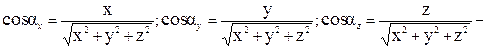
-направляющие косинусы углов между r0 и положительными направлениями осей 0x, 0y, 0z.
Расстояние d между точками P1(x1,y1,z1) и P2(x2,y2,z2) равно
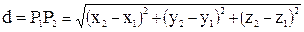
Направленный отрезок (вектор P1P2) может быть записан в виде:
P1P2 = x0(x2 – x1) +y0(y2 – y1) +z0(z2 – z1)
Криволинейная ортогональная система координат
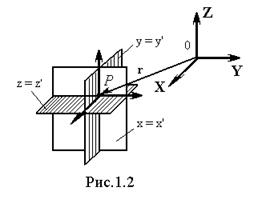 В декартовой прямоугольной системе координат положение в пространстве некоторой точки P(x’, y’, z’) определяется пересечением трех взаимно перпендикулярных координатных плоскостей (рис.1.2)
В декартовой прямоугольной системе координат положение в пространстве некоторой точки P(x’, y’, z’) определяется пересечением трех взаимно перпендикулярных координатных плоскостей (рис.1.2)
x = x’, y = y’, z = z’.
При решении конкретных задач, часто оказывается удобнее определять точку в пространстве не как пересечение трех плоскостей, а как пересечение трех произвольных однозначно заданных произвольных поверхностей, которые в общем случае описываются уравнениями:
q1(x,y,z) = const, q2(x,y.z) = const и q3(x,y.z) = const,
. Для произвольной точки P в системе криволинейных координат устанавливается обозначение P(q1, q2, q3).
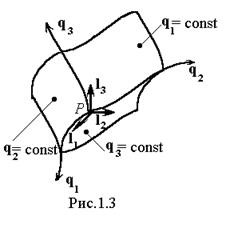 В каждой точке можно рассматривать единичные векторы (орты), касательные координатным линиям и направленные в сторону возрастания соответствующих координат. Будем обозначать их символами l1, l2, l3 (рис.1.3).
В каждой точке можно рассматривать единичные векторы (орты), касательные координатным линиям и направленные в сторону возрастания соответствующих координат. Будем обозначать их символами l1, l2, l3 (рис.1.3).
Как правило, используются только ортогональные системы координат, т.е. такие, орты которых в любой точке взаимно перпендикулярны.Перемещение точки P (рис. 1.4а) выражается приращением ее радиуса-вектора Δr. Разлагая дифференциал dr по ортам l1, l2иl3,имеем: dr = l1d l1+ l2d l2+l3d l3,
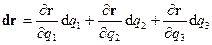 где d l1, d l2 и d l3 – дифференциалы длины по соответствующим криволинейным координатам. С другой стороны:
где d l1, d l2 и d l3 – дифференциалы длины по соответствующим криволинейным координатам. С другой стороны:
Частные производные радиус-вектора r по координатам – это векторы, параллельные их ортам (рис. 1.4б):
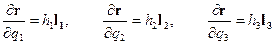
Из сравнения равенств и с учетом последнего, видно, что дифференциалы длины криволинейных координат отличаются от дифференциалов самих координат множителями h1, h2 и h3:
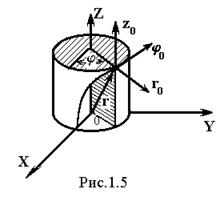 dl1 = h1dq1, dl2 = h2dq2 и dq3 = h3dq3.
dl1 = h1dq1, dl2 = h2dq2 и dq3 = h3dq3.
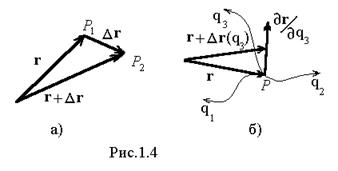 Эти множители называются метрическими коэффициентами, или коэффициентами Ламэ. Цилиндрическая система координат получила свое название от одной из координатных поверхностей, представляющей собой бесконечный круговой цилиндр с радиусом r. Вторая координатная поверхность – полуплоскость, ограниченная осью цилиндра. Третья координатная поверхность – плоскость перпендикулярная оси цилиндра (рис.1.5). Координатные линии цилиндрической системы координат: r – линия пересечения полуплоскости, проходящей через ось Z с плоскостью перпендикулярной оси Z, j – линия пересечения кругового цилиндра с плоскостью перпендикулярной оси Z, z – линия пересечения кругового цилиндра с плоскостью, проходящей через ось цилиндра (образующая цилиндра). Цилиндрические координаты: r (радиус); j (полярный угол); z (аппликата) .Орты r0, j0, z0 образуют правую тройку векторов. Элемент цилиндрической поверхности dS =rdjdz. Элемент объема dV = r dr d
Эти множители называются метрическими коэффициентами, или коэффициентами Ламэ. Цилиндрическая система координат получила свое название от одной из координатных поверхностей, представляющей собой бесконечный круговой цилиндр с радиусом r. Вторая координатная поверхность – полуплоскость, ограниченная осью цилиндра. Третья координатная поверхность – плоскость перпендикулярная оси цилиндра (рис.1.5). Координатные линии цилиндрической системы координат: r – линия пересечения полуплоскости, проходящей через ось Z с плоскостью перпендикулярной оси Z, j – линия пересечения кругового цилиндра с плоскостью перпендикулярной оси Z, z – линия пересечения кругового цилиндра с плоскостью, проходящей через ось цилиндра (образующая цилиндра). Цилиндрические координаты: r (радиус); j (полярный угол); z (аппликата) .Орты r0, j0, z0 образуют правую тройку векторов. Элемент цилиндрической поверхности dS =rdjdz. Элемент объема dV = r dr d 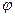 dz.
dz.
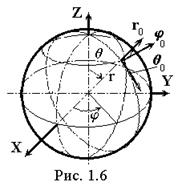 1.1.3 Сферическая система координат получила свое название от одной из координатных поверхностей, представляющей собой сферу радиусом r. Вторая координатная поверхность конус с вершиной, расположенной в начале системы координат и углом вершины равным 2q. Третья – полуплоскость, ограниченная осью Z (рис.1.6). Координатные линии сферической системы координат: r– линия пересечения поверхности конуса с плоскостью, проходящей через ось Z, q – образована пересечением сферы радиуса r с плоскостью, проходящей через ось Z, j– образована пересечением поверхностей сферы и конуса. Сферические координаты: r (радиус); q (меридиональный угол); j (азимутальный угол). Орты r0, q0 ,j0 образуют правую тройку векторов. Элемент сферической поверхности dS = r2 sinq dq dj. Элемент объема dV = r2 sinq dr dq dj.
1.1.3 Сферическая система координат получила свое название от одной из координатных поверхностей, представляющей собой сферу радиусом r. Вторая координатная поверхность конус с вершиной, расположенной в начале системы координат и углом вершины равным 2q. Третья – полуплоскость, ограниченная осью Z (рис.1.6). Координатные линии сферической системы координат: r– линия пересечения поверхности конуса с плоскостью, проходящей через ось Z, q – образована пересечением сферы радиуса r с плоскостью, проходящей через ось Z, j– образована пересечением поверхностей сферы и конуса. Сферические координаты: r (радиус); q (меридиональный угол); j (азимутальный угол). Орты r0, q0 ,j0 образуют правую тройку векторов. Элемент сферической поверхности dS = r2 sinq dq dj. Элемент объема dV = r2 sinq dr dq dj.
Сведения о декартовой, цилиндрической и сферической системах координат сведены в таблицу 1.
Таблица 1
| Номер координаты, i | Система координат | |||||||||||
| декартова | цилиндрическая | сферическая | ||||||||||
| qi | li | hi | dli | qi | li | hi | dli | qi | li | hi | dli | |
| x | x0 | dx | r | r0 | dr | r | r0 | dr | ||||
| y | y0 | dy | j | j0 | r | rdj | q | q0 | r | rdq | ||
| z | z0 | dz | z | z0 | dz | j | j0 | r sinq | r sinqdj |
Где: h1, h2 и h3 – коэффициенты Ламе, связывающие дифференциалы длины криволинейных координат с дифференциалами самих координат
dli = hidqi
Дата добавления: 2016-03-27; просмотров: 3619;
