Векторное поле и векторные (силовые) линии

Если во всех точках некоторой области пространства определены значения вектора А(r), говорят, что в данной области задано поле вектора А(r) (векторное поле А(r)). Любой вектор А(r) можно представить в виде

A(r) = l₁A₁(r) + l₂A₂(r) + l₃A₃(r),

то задание вектора А(r) эквивалентно заданию трех скалярных функций A₁(r), A₂(r) и A₃(r).

Потенциальные векторные поля. Если задана векторная функция F, являющаяся градиентом некоторой скалярной функции y, то такое векторное поле называется потенциальным, а y – потенциалом. Поверхности уровня, на которых y =const, являются, следовательно, поверхностями постоянного потенциала, или эквипотенциальными поверхностями. Линии вектора F = grad y всегда ортогональны эквипотенциальным поверхностям, т.е. пересекают их под прямым углом.

Для наглядного изображения векторного поля строят так называемые векторные линии (рис. 2.9), т.е. линии, в каждой точке которых вектор направлен по касательной к линии 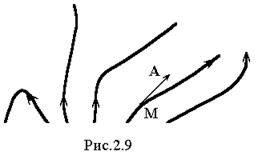.Введем понятие векторного дифференциала длины вдоль некоторой линии:

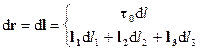
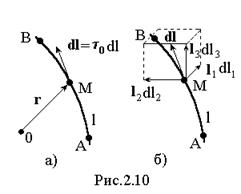В первой строчке он выражен через обычный дифференциал длины и единичный вектор касательной t₀ (рис. 2.10а), а во второй – через дифференциалы и единичные векторы ортогональной системы координат (рис. 2.10б). области пространства, в которой задано поле вектора F, проведем некоторую непрерывную кривую (контур l), соединяющую точки А и В (рис.2.12). Направление от А к В будем считать положительным. Рассмотрим криволинейный интеграл, вычисляемый вдоль некоторого пути по кривой l от точки А до точки В

.

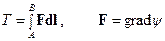Раскрывая скалярное произведение в подынтегральном выражении

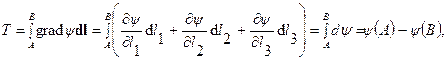
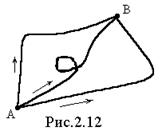т.е. интеграл Т при однозначности y не зависит от пути, а определяется только значениями потенциала y в начальной и конечной точках пути. Каков бы ни был путь интегрирования, ведущий от точки А к точке В (рис.2.12), значение Т остается равным разности потенциалов в этих точках.

Из этого следует, что интеграл по замкнутому пути L равен нулю:

,

поскольку точки А и В в данном случае совпадают. Этот интеграл называется циркуляцией вектора F по замкнутому контуру (пути) L. Циркуляция градиента тождественно равна нулю.

Справедливо и обратное утверждение. Если циркуляция вектора F по любому замкнутому контуру равна нулю, то вектор F может быть представлен в виде F = grad y.

2.1.3Дивергенция.Силовые линии и поток вектора. 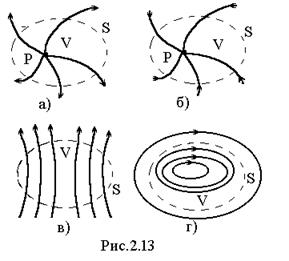Выделим некоторый объем V, охватываемый замкнутой поверхностью S в области пространства, в каждой точке которого задано векторное поле F. На рис. 2.13 изображено несколько характерных типов расположения силовых линий, которые могут встретиться (пунктиром изображена граница S объема V). Внутри объема V может находиться «источник» векторных линий (рис. 2.13а), либо «сток» (рис. 2.13б), т.е. линии выходят из V или, соответственно входят в V через границу S. Но векторные линии могут также пронизывать V насквозь, не начинаясь и не кончаясь в этой области (рис. 2.13в). Наконец, замкнутые векторные линии могут совершенно не пересекать границу S (рис. 2.13г).

Характер поведения векторного поля можно оценить с помощью потока вектора. Потоком вектора F через поверхность S называется интеграл

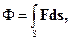
где векторный дифференциал ds это произведение обычного дифференциала ds на единичный вектор нормали n₀ к поверхности, т.е. ds = n₀ds. Тогда F ds = F n₀ ds = F_n ds. В случае замкнутой поверхности положительной нормалью n₀ всегда считается внешняя нормаль. В случае незамкнутой поверхности S выбирается одно из двух возможных направлений нормали. В теории электромагнитного поля положительной считают нормаль к поверхности S, опирающейся на одновитковый замкнутый контур L если из конца нормали n₀ обход контура виден идущим против часовой стрелки (нормаль и обход контура как бы образовывают правовинтовую систему).

Скалярное произведение под знаком интеграла в будет положительным когда угол между векторами F и ds острый, и отрицательным при тупом угле.

Дивергенция вектора F в точке P, обозначаемая divF, это предел отношения потока вектора F через замкнутую поверхность DS, охватывающую точку P, к объему DV, ограниченному поверхностью DS при стягивании его к точке М.

.

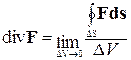В тех точках, в которых div F ¹ 0, линии вектора F претерпевают разрыв. Линии выходят из точек, где div F > 0 – источники (рис. 2.1а) и входят в точки, где div F < 0 – стоки (рис. 2.1б), в точках, где div F= 0, линии вектора F непрерывны. Мерой интенсивности истока (стока) служит div F.

Дивергенция в криволинейных ортогональных координатах

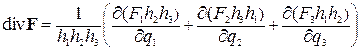
Дивергенция в декартовых координатах:

;

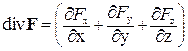в цилиндрической системе координат:

;

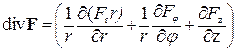в сферической системе координат:

.

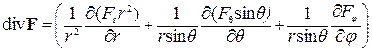Свойства дивергенции.

div (A + F) = div A + div F ,

div(cF) = c ^. div F ,

если j – скалярная, а F – векторная функции координат, то

div (j ^. F) = j ^. div F + (gradj , F).

Теорема Остроградского-Гаусса.

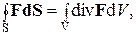
Пользуясь этой формулой, следует помнить. что S –замкнутая поверхность, ограничивающая объем V, dS = n₀ dS, где dS – элемент поверхности, а n₀ – орт внешней нормали к поверхности S.