Метод комплексных амплитуд .
Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических во времени электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют монохроматическими. В буквальном переводе «монохроматический» означает «одноцветный». Название взято из оптики: как известно, каждому цвету соответствуют колебания определенной частоты. Анализ гармонических процессов существенно упрощается при использовании метода комплексных амплитуд.
Если некоторая величина u(t) изменяется во времени по закону
u(t) = umcos(ωt + φ)
то говорят, что происходят гармонические колебания, причем um называется амплитудой, ω – круговой частотой, а аргумент косинуса ωt + φ – фазой колебания (полной фазой); последняя, если это требуется, приводится к значению, лежащему в пределах 0 ÷ 2π или – π ÷ π; величину φ называют начальной фазой ( а также фазовым сдвигом или просто фазой) Наименьший отрезок времени T, обладающий тем свойством что для любого момента t
u(t + T) = u(t),
есть по определению, период колебаний, а число периодов в секунду – частота, обозначаемая f. Очевидно
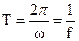 .
.
В теории электромагнитного поля встречаются, в частности, скалярные функции координат и времени вида
u(r,t) = u(x,y,z) = um(r) cos[ωt + φ(r)],
описывающие гармонические колебания в пространстве с амплитудами и фазами, которые могут изменяться от точки к точке. Три такие скалярные функции иногда являются компонентами вектора в декартовой или иной системе координат. Такой вектор может быть представлен в виде:
V(r,t) = x0Vmx(r) cos[ωt + φx(r)] + y0Vmy(r) cos[ωt + φy(r)] +z0Vmz(r) cos[ωt + φz(r)].
В частности, если φx = φy = φz, т.е., как говорят, все компоненты вектора колеблются «в одной фазе», то
V(r,t) = Vm(r) cos[ωt + φ(r)],
где Vm(r) = x0Vmx(r) + y0Vmy(r) +z0Vmz(r) – амплитуда колеблющегося вектора. В дальнейшем в подобных выражениях для краткости будем опускать аргументы (r,t) и (r).
Введем комплексную функцию 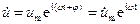 , где i– мнимая единица (i2 = –1), множитель
, где i– мнимая единица (i2 = –1), множитель 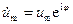 называется комплексной амплитудой колебаний. Для перехода от комплексной функции
называется комплексной амплитудой колебаний. Для перехода от комплексной функции 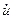 к функции u нужно взять от
к функции u нужно взять от 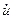 реальную часть
реальную часть
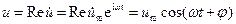
Как видно, в комплексном представлении 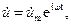 мы имеем произведение функции координат
мы имеем произведение функции координат 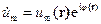 и функции времени eiωt. Совершенно аналогично
и функции времени eiωt. Совершенно аналогично
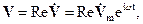
где комплексная амплитуда (функция координат) 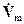 есть
есть
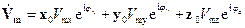 ,
,
а в частном случае
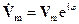 .
.
Комплексная амплитуда несет информацию как об амплитуде так и о начальной фазе колебаний (трех начальных фазах в общем случае вектора).
Пусть имеется линейное уравнение
L (V) = F, ( 1 )
где V– неизвестная векторная функция вида, L – некоторый линейный вещественный дифференциальный или интегральный оператор, а F заданная векторная функция того же вида, что и V:
F = x0Fmx cos(ωt + φx) + y0Fmy cos(ωt + φy) +z0Fmz cos(ωt + φz).
Заметим, что векторное уравнение взято в качестве более общего случая, и все дальнейшие рассуждения применимы и к скалярным уравнениям.
Рассмотрим новое уравнение:
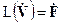 . ( 2 )
. ( 2 )
В силу линейности оно распадается на два уравнения относительно действительных и мнимых частей входящих функций
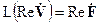
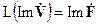 ,
,
причем первое из этих уравнений не отличается от (1), поскольку 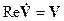 и
и 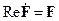 . Это означает, что вещественная часть решения уравнения (2) удовлетворяет первоначальному уравнению (1).
. Это означает, что вещественная часть решения уравнения (2) удовлетворяет первоначальному уравнению (1).
Очевидно, что вместо (1) можно решать уравнение (2) и затем разыскиваемую функцию V получать как вещественную часть найденного решения 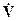 . Преимущество такого подхода – в исключении временной зависимости. Действительно, операции дифференцирования и интегрирования по времени под знаком оператора L в (2) сводятся к умножению и, соответственно, делению функции
. Преимущество такого подхода – в исключении временной зависимости. Действительно, операции дифференцирования и интегрирования по времени под знаком оператора L в (2) сводятся к умножению и, соответственно, делению функции 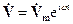 на iωt так что
на iωt так что
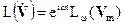 ,
,
где Lω – зависящий от ω оператор, который выражает либо дифференцирование или (и) интегрирование по координатам. Внося это в (2) и исключая слева и справа общий множитель eiωt, имеем:
 . (3)
. (3)
Таким образом, вместо первоначального уравнения (1) относительно функции координат и времени V(r,t) получили уравнение (3) относительно комплексной амплитуды 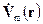 , функции координат.
, функции координат.
Метод комплексных амплитуд состоит в том, что заданное уравнение типа (1) приводится к виду (3), а после того как оно решено, и функция координат найдена, разыскиваемая функция координат и времени V(r,t) получается как вещественная часть от  .
.
Средние значения
Говорят, что величина u(t1) есть «мгновенное значение» функции u(t) для момента t1. Но часто представляет интерес также среднее значение F, под которым понимают
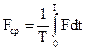 .
.
Очевидно, в частности, что для F= u
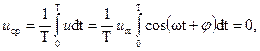
Дата добавления: 2016-03-27; просмотров: 1657;
