Асимптотические формулы Муавра-Лапласа.

Теорема 1. Локальная теорема Муавра-Лапласа.Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний п достаточно велико, то вероятностьP_n(k) того, что событие А появиться в n испытаниях ровно k раз приближенно равна

(1)

где 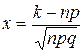. Причем это равенство тем точнее, чем больше n.

Имеются специальные таблицы, в которых помещены значения функции 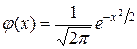(функция Гаусса), соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 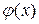четна, т. е. 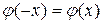. При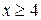

Пример 1.Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию, n = 400; k = 80; р = 0,2; q = 0,8. Вос­пользуемся асимптотической формулой Лапласа:

Вычислим х: 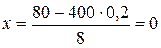. По таблице находим 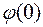= 0,3989. Искомая вероятность

.

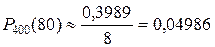Формула Бернулли приводит примерно к такому же результату:

.

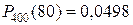Пример 2.Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. По условию, n =10; k = 8; р = 0,75; q = 0,25. Воспользуемся асимптотической формулой Лапласа:

.

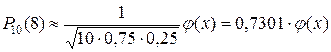Вычислим х: 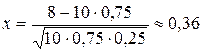. По таблице находим 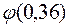= 0,3739. Искомая вероятность

.

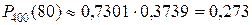Формула Бернулли приводит к иному результату, а, именно . Столь значительное расхождение ответов объясняется тем, что в настоящем примере п имеет малое значение (формула Муавра-Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п).

Теорема 2. Интегральная теорема Муавра-Лапласа.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля, и единицы, а число независимых испытаний п достаточно велико, то вероятность Р_п (k_l, k₂) того, что событие А появится в п испытаниях от k₁ до k₂ раз (не менее k₁ и не более k₂), приближенно равна определенному интегралу

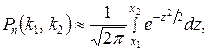(2)

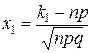где и 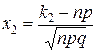. Причем это равенство тем точнее, чем больше n.

При решении задач, требующих применения интегральной теоремы Муавра-Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 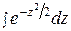не выражается через элементарные функции. В таблице даны значения функции Лапласа 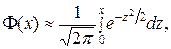дляположительных значений х и для х = 0; для х < 0 пользуются той же таблицей, функция Ф (x) нечетна, т.е. 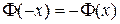. В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф(х) = 0,5.

Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (2) так:

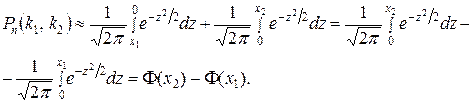
Итак,вероятность того, что событие А появится в п независимых испытанияхот k₁до k₂раз,

где 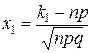и .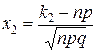

Пример.Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию, р = 0,2; q = 0,8; n = 400; k₁= 70; k₂=100. Воспользуемся интегральной теоремой Лапласа. Вычислим нижний и верхний пределы интегрирования:

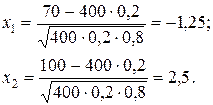
Таким образом, имеем

Р₄₀₀(70, 100)=Ф(2,5) - Ф(- 1,25) = Ф(2,5) + Ф(1,25). По таблице находим:

Ф (2,5) = 0,4938; Ф( 1,25) = 0,3944.

Искомая вероятность

Р₄₀₀(70, 100)=0,4938 + 0,3944=0,8882.

Замечание.С помощью функции Лапласа можно найти вероятность отклонения относительной частоты от вероятности р в п независимых испытаниях, используя формулу: 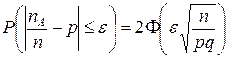, где 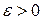- некоторое число.