Стандартное нормальное распределение

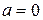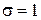Нормальное распределение при и называется стандартным нормальным распределением. Плотность стандартного нормального распределения имеет вид:

,

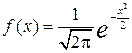а функция распределения

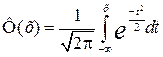
называется функцией Лапласа.

Свойства функции Лапласа:

1. Функция Лапласа является табулированной, то есть ее значения приведены в таблицах (приложение 2). Она принимает значения от 0 до 0,5, то есть .

2. Функция нечетная, .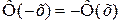

3. Вероятность попадания СВ на заданный интервал :

.

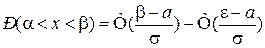4. Вероятность отклонения СВ от своего математического ожидания

.

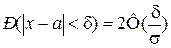Пусть требуется найти вероятность попадания СВ на заданный интервал, симметричный относительно ее математического ожидания 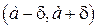. По предыдущей формуле имеем:

.

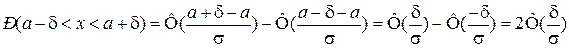Замечание. Иногда в качестве функции Лапласа берут функцию

,

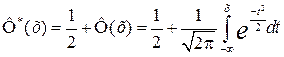тогда 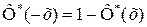, значения этой функции принадлежат промежутку от 0 до 1: .

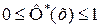Пример.Найти вероятность попадания в интервал 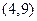значений нормальной случайной величины 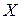, для которой математическое ожидание 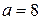, среднее квадратическое отклонение .

Решение.Применим формулу:

;

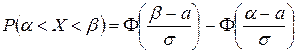в данном случае она примет вид:

.

Функция Лапласа является нечетной, поэтому

.

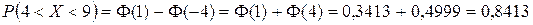Значения 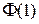, найдены по таблице значений функции Лапласа (приложение 2).

Правило трех сигм

Сформулируем теперь «правило трёх сигм»: практически достоверно, что если случайная величина распределена нормально, абсолютное отклонение ее от математического ожидания не превосходит утроенного среднеквадратического отклонения:

.

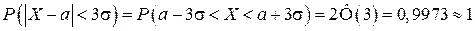Или – вероятность того, что случайная величина отклониться от своего математического ожидания на величину, большую утроенного среднеквадратического отклонения, равна:

.

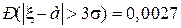Смысла в запоминании числа 0,0027 нет никакого, а вот помнить, что почти вся масса нормального распределения сосредоточена в границах 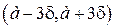, всегда полезно.