Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Приведенная формулировка справедлива только для дискретных случайных величин.
Для непрерывных величин
∞
М[Х] = ∫ x f(x)dx, где f(x) - плотность распределения Х.
-∞
Существуют различные способы расчета среднего значения. Наиболее распространенными формами представления средних величин являются среднее арифметическое значение, медиана и мода.
Среднее арифметическое получается путем деления суммарной величины данного признака для всей однородной статистической совокупности на количество единиц этой совокупности. Для расчета среднего арифметического используется формула:
Хср = (Х1+Х2+... +Хn):n,
где Хi - значение признака у i-ой единицы совокупности, n - количество единиц совокупности.
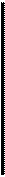Модой случайной величины называется ее наиболее вероятное значение.
 |
М
 |
М
Медианой называется значение, которая расположена в середине упорядоченного ряда. Для нечетного количества единиц ряда медиана является единственной и находится точно в середине ряда, для четного - она определяется как среднее значение двух рядом расположенных единиц совокупности, занимающих среднее положение.
Часто применяется еще одна характеристика положения - медиана случайной величины.
Медианой сл.в. называется такое ее значение Ме для которого
P(X< Ме)= P(X> Ме)
 |
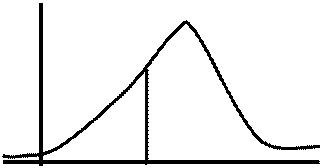Ме
Моменты. Дисперсия. СКО.
Кроме характеристик положения Сл.в. используются характеристики, которые называются моментами.
На практике используются моменты двух видов: начальные и центральные.
Начальным моментом s-го порядка дискретной случайной величиныпорядка называется сумма вида:
n
αs[X]= ∑xispi
i=1
Начальным моментом s-го порядка случайной величины Х называется математическое ожидание s-й степени этой случайной величины
αs[X]=М[Xs]
Для определения центральных моментов необходимо дать определение центрированной случайной величины.
Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от ее МОЖ
ο
Х = Х-mx
Моменты центрированной случайной величины порядка S называются центральными моментами.
Центральным моментом s-го порядка случайной величины Х называется математическое ожидание s-й степени соответствующей центрированной случайной величины:
o
μs[X]= М[Xs]= М[(Х-Mx)s]
Для дискретной случайной величины s-й центральный момент равен
n
μs= ∑(xi- mx) spi
i=1
Для любой случайной центральный момент первого порядка равен нулю.
Второй центральный момент называется дисперсией.Эта характеристика является очень важной и для нее введено специальной обозначение
o
μ2=D[X]; D[X]= М[X2]
Дисперсией случайной величины называется МОЖ квадрата соответствующей центрированной величины.
n
D[X]= ∑(xi- mx) 2pi
i=1
Дисперсия случайной величины характеризует рассеивание (разбросанность) значений случайной величины около ее МОЖ.
Дисперсия имеет размерность квадрата случайной величины. Часто удобнее пользоваться величиной размерность, которой совпадает с размерностью случайной величины. Для этого из дисперсии надо извлечь квадратный корень. Полученная величина называется СКО(среднеквадратическое отклонение)
σ[X] = √D[X]
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Задача проверки правдоподобия гипотез |
Дата добавления: 2016-02-20; просмотров: 1107;