Алгоритм разложения чисел на простые множители.

Алгоритм А (Разложение на простые множители путем деления). По данному положительному целому числу N этот алгоритм находит простые множители p₁ ≤ р₂ ≤ … ≤ p_t числа N. В этом методе используется вспомогательная последовательность пробных делителей

d = d₀ < d₁ < d₂ < d₃ < …,

которая включает в себя все простые числа < 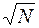(и, если это удобно, может содержать числа, не являющиеся простыми). Последовательность чисел d_i должна также содержать по крайней мере одно значение, такое, что d_k > .

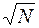А1. [Начальная установка.] Присвоить t ← 0, k ← 0, n ← N. (В ходе выполнения алгоритма переменные t, k, n подчинены следующим условиям: "n = N/p₁...p_t и n не имеет простых множителей, меньших d_k".)

А2. [n = 1?] Если n = 1, алгоритм заканчивается.

A3. [Разделить.] Присвоить q ← 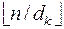, r ← n mod d_k. (Здесь q и r - соответственно частное и остаток от деления числа n на d_k.)

А4. [Остаток равен нулю?] Если r ≠ 0, то перейти к шагу А6.

А5. [Множитель найден.] Увеличить t на 1 и присвоить p_t ← d_k, n ← q. Возвратиться к шагу А2.

А6. [Частное мало?] Если q > d_k, увеличить k на 1 и возвратиться к шагу A3.

А7. [n — простое число.] Увеличить t на 1, присвоить p_t ← n и завершить выполнение алгоритма.

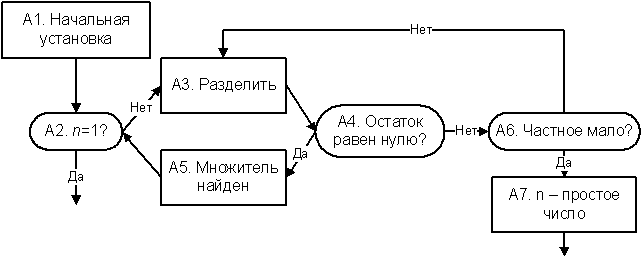
Рис.32. Алгоритм разложения числа на простые множители.

Пример.

Разложение на простые множители числа N = 25852. Сразу же находим, что N = 2 · 12926; следовательно, р₁ = 2. Далее, 12926 = 2 · 6463, так что р₂ = 1. Но теперь число n = 6463 не делится на числа 2, 3, 5, ..., 19; находим, что n = 23 · 281; значит, р₃ — 23. В итоге имеем 281 = 12 · 23 + 5 и 12 ≤ 23, т. е. р₄ = 281.

Алгоритм Евклида.

Разделить целое число a на число b с остатком – это значит найти такие числа q и r c 0 £ r < |b|, при которых выполняется равенство

a = q · b + r.

Разделить многочлен f на многочлен g с остатком – это значит найти такие многочлены q и r c 0 £ deg r < deg g, при которых выполняется равенство

f = q · g + r.

Для вычисления НОД(r₀ = a, r₁ = b) производится деление с остатком по следующей схеме:

a = r₀ = q₁r₁ + r₂,

b = r₁ = q₂r₂ + r₃,

.....

r_m-2 = q_m-1b_m-1 + r_m,

r_m-1 = q_mr_m.

Работа алгоритма Евклида основана на том, что отображение 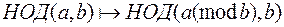сохраняет наибольший общий делитель.

Отображение работает до a = НОД, b = 0.

Пример.

НОД(21, 12) = НОД (21 (mod 12), 12) =

= НОД(12, 9) = НОД (12 (mod 9), 9) =

= НОД(9, 3) = НОД (9 (mod 3), 3) =

= НОД(3, 0) = 3

Работа бинарного алгоритма нахождения НОД основана на следующем ряде отображений, также сохраняющих НОД:

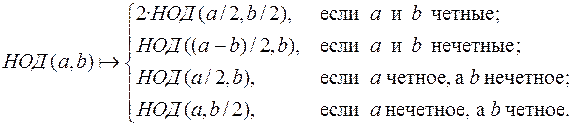
Отображения работают до (a – b) /2 = 0. НОД = b.

Пример.

НОД(21, 12) = НОД (21, 12 / 2) =

= НОД(21, 6) = НОД (21, 6 / 2) =

= НОД(21, 3) = НОД ((21 – 3) / 2, 3) =

= НОД(9, 3) = НОД ((9 – 3) / 2, 3) =

= НОД(3, 3) = НОД ((3 – 3) / 2, 3) =

= НОД(0, 3) = 3

Во всех вышеперечисленных рассуждениях принимается a ³ b.