ПРИНЦИПЫ ПОСТРОЕНИЯ АСИММЕТРИЧНЫХ КРИПТОГРАФИЧЕСКИХ АЛГОРИТМОВ

4.1. Математические основы асимметричной криптографии.

4.1.1. Свойства операций, определенных на некотором множестве

4.1.2. Функция Эйлера. Поле. Теоремы Эйлера - Лагранжа и Ферма.

4.1.3. Конечные поля.

4.1.4. Основные алгоритмы.

4.1.5. Алгоритмы нахождения НОД и мультипликативного обратного по модулю.

4.1.6. Китайская теорема об остатках.

4.1.7. Символы Лежандра и Якоби. Извлечение корней.

4.2. Примеры современных асимметричных шифров.

4.2.1. Криптосистема RSA.

4.2.2. Взаимосвязь компонентов RSA.

4.2.3. Криптосистема Эль-Гамаля.

4.2.4. Криптосистема Рабина.

4.2.5. Рюкзачные криптосистемы.

4.2.6. Шифрсистема Мак-Элиса.

Математические основы асимметричной криптографии.

Преимущество систем с открытым ключом состоит в том, что ключ не требуется сохранять в тайне. Необходимо лишь обеспечить его аутентичность, что сделать, как правило, легче, чем обеспечить рассылку секретных ключей.

Системы шифрования с открытым ключом осуществляют блочное шифрование, поэтому открытый текст перед шифрованием разбивается на блоки.

Ассиметричные системы шифрования обеспечивают значительно меньшие скорости шифрования, нежели симметричные, в силу чего они обычно используются не для шифрования сообщений, а для шифрования пересылаемых сеансовых секретных ключей, которые затем используются в симметричных системах шифрования.

Для понимания принципов построения асимметричных криптосистем необходимо повторить некоторые понятия алгебры и алгоритмы теории чисел.

Свойства операций.

Рассмотрим основные свойства арифметических операций определенных на некотором множестве А.

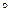*, - обозначение операций.

Замкнутость: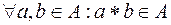

Ассоциативность: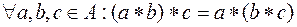

Наличие нейтрального элемента Q Î A: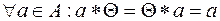

Существование обратного элемента 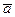Î A:

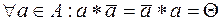
Коммутативность: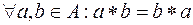

Дистрибутивность операции 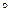относительно операции *: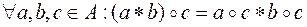

Группы, кольца.

Определение. Группа – множество G с операцией, которая: замкнута, обладает нейтральным элементом, ассоциативна, относительно нее каждый элемент обладает обратным. Группу с коммутативной операцией называют коммутативной или абелевой.

Практически все группы в криптографии – абелевы. Обозначение группы: (G, знак операции).

Мультипликативная группа (G, · ):

Групповая операция – умножение · ;

Нейтральный элемент – единица 1 ;

Обратный элемент – a^-1;

Многократное применение операции – возведение в степень

a⁵ = a · a · a · a · a.

Аддитивная группа (G, + ):

Групповая операция – сложение + ;

Нейтральный элемент – ноль 0 ;

Обратный элемент – – a;

Многократное применение операции – умножение

5 · a = a + a + a + a + a.

Образующая g – такой элемент группы, что любой другой элемент может быть получен путем многократного применения к нему групповой операции. Запись .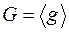

В мультипликативной группе: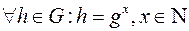

В аддитивной группе: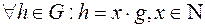

Определение. Кольцо – множество R с двумя операциями: сложением и умножением, в котором обе операции замкнуты, ассоциативны, обладают нейтральным элементом, связаны законом дистрибутивности, а сложение коммутативно и для каждого элемента есть обратный по сложению. Обозначение кольца (R, ·, +).

В коммутативном кольце операция умножения дополнительно обладает свойством коммутативности.

Основное кольцо, важное для криптологии – коммутативное кольцо остатков от деления на натуральное число n, большее 1, которое также называют кольцом вычетов по модулю n и обозначают Z_n или Z/nZ.