Примеры современных асимметричных шифров.

Криптосистема RSA.

Система построена на следующих функциях:

Односторонняя функция - умножение двух больших простых чисел:

N = p · q.

Обратная задача – задача факторизации, является сложной.

Односторонняя функция с секретом - потенцирование (возведение в степень) по модулю составного N = p · q сфиксированной степенью E:

C = m^E mod N.

Обратная задача – задача извлечения корня степени E по модулю N:

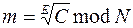
является сложной, если неизвестно разложение N на множители (секрет) и является простой при известном разложении N.

В дальнейшем секретные элементы криптосистем обозначаются строчными (p, q, m и пр.) открытые прописными (N, C, E и пр.) латинскими буквами.

Предположим абонент A считает нужным разрешить всем желающим отправлять ему секретные сообщения, расшифровать которые способен только он. Для этого выбирается два больших простых числа p и q, которые держатся в секрете, и публикуется их произведение

N = p · q,

которое называют модулем алгоритма. Кроме того, выбирается шифрующая экспонента E, удовлетворяющая условию

НОД (E, (p – 1), (q – 1)) = 1.

Как правило E берут равным 3, 17 или 65537. Пара, доступная всем желающим, - это (N, E). Для выбора секретного ключа применяют расширенный алгоритм Евклида к паре чисел E и

(p – 1)(q – 1), получая при этом расшифровывающую экспоненту d. Найденная экспонента удовлетворяет соотношению

E · d = 1 (mod (p – 1)(q – 1)) = 1.

Секретным ключом является тройка (d, p, q). Фактически, можно было бы выбросить простые делители p и q из ключа и помнить лишь о d и всем числе N. Но, как будет рассмотрено позднее, это снизит скорость алгоритма.

Допустим теперь пользователь B намерен зашифровать сообщение, адресованное A. Он сверяется с открытым ключом и представляет сообщение в виде числа m, строго меньшего модуля N алгоритма. Шифртекст C получается из m по следующему правилу:

C = m^E (mod N).

A, получив шифрограмму, расшифровывает ее, возводя число C в степень d:

m = C^d (mod N).

Равенство имеет место в связи с тем, что порядок группы

#(Z/NZ)^* = φ(N) = (p – 1)(q – 1).

Потому по теореме Лагранжа (Эйлера-Ферма),

x^{(p - 1)(q - 1)} = 1 (mod N)

для любого числа x Î (Z/NZ)^*. Поскольку E и d взаимно обратны по модулю (p – 1)(q – 1), при некотором целом числе s получается равенство

Ed – s(p – 1)(q – 1) = 1.

Следовательно,

C^d = (m^E)^d = m^Ed = m^{1 + s(p – 1)(q – 1)} = m · m ^{s(p – 1)(q – 1)} = m (mod N).

Пример. Пусть p = 7 и q = 11. Тогда N = 77, а (p – 1)(q – 1) = 6 · 10 = 60. В качестве открытой шифрующей экспоненты возьмем число E = 37, поскольку НОД(37, 60) = 1. Применяя расширенный алгоритм Евклида, найдем d = 13, так как

37 · 13 = 481 = 1 (mod 60).

Для зашифрования сообщения численное представление которого имеет вид m = 2:

C = m^E (mod N) = 237 (mod 77) = 51.

Расшифрование происходит аналогично:

m = C^d (mod N) = 5113 (mod 77) = 2.