Криптосистема Эль-Гамаля.

x = ind _G,P H

является сложной.

Здесь опишем шифрование по Эль-Гамалю, использующее конечные поля. Существует и аналогичная система на эллиптических кривых.

В отличие от RSA, в алоритме Эль-Гамаля существуют некоторые открытые параметры, которые могут быть использованы большим числом пользователей. Они называются параметрами домена и выглядят следующим образом:

- P – «большое простое число», то есть число, насчитывающее около 1024 бит, такое, что P – 1 делится на другое, «среднее простое число» Q, лежащее неподалеку от 2¹⁶⁰.

- G – элемент мультипликативной группы поля 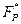, порядок которой, как мы знаем делится на Q, причем

G^{(P – 1)/Q} (mod P) ≠ 1.

Все параметры домена, то есть P, Q и G, выбираются таким образом, чтобы элемент G^{(P – 1)/Q} был образующей абелевой группы A порядка Q. Информация об этой группе открыта и используется большим числом пользователей.

После выбора параметров домена определяют открытый и закрытый ключи. Закрытым ключом может априори быть любое натуральное число x, а открытый ключ получается по следующей формуле:

H = G^x (mod P).

Обратите внимание на то, что каждый из пользователей RSA должен генерировать два больших простых числа для определения ключевой пары, что является довольно громоздкой задачей, а в системе Эль-Гамаля для построения ключевой пары достаточно найти какое-нибудь случайное число и сделать сравнительно несложные вычисления в арифметике остатков.

Сообщение в этой ситеме представляется ненулевым элементом поля 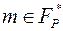. Для его шифрования поступают следующим образом:

- генерируют случайный эфемерный ключ k,

- вычисляют C₁ = G^k,

- находят C₂ = m · H^k,

- выдают получившийся шифртекст в виде пары С = (С₁, С₂).

Заметим, что при каждом шифровании применяется свой кратковременный ключ k. Поэтому, шифруя одно сообщение дважды, мы получаем разные шифртексты.

Чтобы расшифровать пару данных С = (С₁, С₂), производят следующие преобразования:

Пример. Q = 101, P = 809 и G = 3.

Легко проверить, что Q действительно делит число P – 1, а порядок элемента G в группе 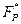делится на Q. Порядок элемента G равен 808, поскольку

3⁸⁰⁸ = 1 (mod P),

и ни при каких меньших степенях такого равенства не получается.

В качестве пары открытого и закрытого ключа выберем

x = 68 и H = G^x = 3⁶⁸ = 65 (mod P).

Допустим, нам нужно зашифровать сообщение, численное представление которого равно

m = 100. Поступаем следующим образом.

- Генерируем случайный эфемерный ключ k = 89.

- Находим С₁ = G^k = 3⁸⁹ = 345 (mod P).

- Получаем С₂ = m · H^k = 100 · 65⁸⁹ = 517 (mod P).

- Отправляем шифртекст C = (345, 517).

Адресат сможет восстановить текст, делая также вычисления:

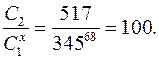
Последнее равенство получается чуть более сложно, чем в вещественных числах: сначала число 345 возводится в степень 68 по модулю 809, вычисляется мультипликативный обратный к результату по этому же модулю, а затем найденный обратный умножается на 517.