Криптосистема Меркля-Хеллмана.
Предположим, что элементы открытого текста имеют в качестве своих числовых эквивалентов k-разрядные двоичные числа n.
Каждый пользователь выбирает быстрорастущий набор {v0, …, vk – 1}, целое число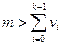 
и целое число a, такое что a < 0 < m и НОД(a, m) = 1.
После этого вычисляются b = a -1 (mod m) и k-элементный набор {Wi} = {W0, …, Wk –1}, пределяемый равенствами Wi = avi (mod m). Пользователь держит числа {vi}, m, a и b в секрете, а набор {Wi} делает общеизвестным. Таким образом, ключом зашифрования является набор
{W0, …, Wk –1},
а ключом расшифрования – пара
(b, m),
которая вместе с ключом зашифрования позволяет определить набор {v0, …, vk – 1}.
Желающий передать сообщение n = (n0… nk – 1)2 пользователю с ключом шифрования {Wi} вычисляет
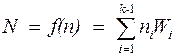
и передает это число.
Чтобы прочесть это сообщение, пользователь сначала находит s = bC:
,
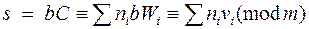поскольку bWi ≡ bavi ≡ vi (mod m). Теперь можно воспользоваться приведенным выше алгоритмом для быстровозрастающего рюкзака и найти единственное решение
(n0… nk – 1)2 = n задачи о подмножестве {vi} с суммой равной s.
Пример. Элементы открытого текста – двоичные представления букв 26-буквенного алфавита от «A» = 0 = (00000)2 до «Z» = 25 = (11001)2 .
Cекретный быстровозрастающий набор {v0, …, vk – 1} = {2, 3, 7, 15, 31}.
Выберем m = 61, a = 17, тогда b = 18 и открытый ключ шифрования
{W0, …, Wk –1} = {34, 51, 58, 11, 39}.
Чтобы послать сообщение «WHY» корреспондент должен вычислить:
«W» = (10110)2 ® 51 + 58 + 39 = 148,
«H» = (00111)2 ® 34 + 51 + 58 = 143,
«Y» = (11000)2 ® 11 + 39 = 50.
N = n1, n2, n3 = 148, 143, 50.
Чтобы прочитать сообщение N, сначала умножают эти числа на 18 и приводят результаты по модулю 61, получают S = s1, s2, s3 = 41, 12, 46 далее, пользуясь алгоритмом для быстрорастущего рюкзака для всех si, восстанавливают сообщение
(10110)2, (00111)2, (11000)2
Дата добавления: 2016-02-13; просмотров: 1759;