Криптосистема Рабина.
Система базируется на трудности задачи факторизации больших целых чисел, а точнее на трудности извлечения квадратного корня по модулю составного числа N = p · q.
Эти задачи эквивалентны:
- зная простые делители числа N, можно легко извлекать корни по модулю N,
- умея извлекать корни по модулю N, можно легко разложить N на составные множители.
Такую систему можно считать в некотором отношении более криптостойкой, чем RSA. Процесс шифрования в системе Рабина происходит намного быстрее, чем практически в любой другой криптосистеме с открытым ключом. Однако, не смотря на эти преимущества, система Рабина используется все же реже чем RSA.
Выбираются два простых числа p и q, удовлетворяющие условию
p = q = 3 (mod 4).
Такой специальный вид чисел сильно ускоряет процедуру извлечения корней по модулю p и q. Закрытым ключом системы является пара
(p, q).
Для определения соответствующего открытого ключа берут произведение N = p · q и генерируют случайное целое число B Î {0, …, N – 1}. Открытый ключ это пара
(N, B).
Для шифрования сообщения m в алгоритме Рабина вычисляют
C = m(m + B) (mod N).
Таким образом, шифрование состоит из операции сложения и умножения по модулю N, что обеспечивает более высокую скорость шифрования, чем в RSA, даже если в последней выбирают небольшую шифрующую экспоненту.
Расшифрование в этом алгоритме гораздо более сложное. По существу нужно вычислить
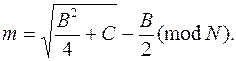
На первый взгляд здесь не требуется никакой секретной информации, но, очевидно, для извлечения корней по модулю N очень и очень полезно знать разложение N на простые множители. Поскольку N – произведение двух простых чисел, существует четыре возможных квадратных корня из числа по модулю N. Поэтому при расшифровании получается четыре возможных варианта открытого текста. Чтобы выбор был более определенным, стоит к открытому тексту добавлять некую избыточную информацию.
Объясним, почему при расшифровании мы действительно получаем m. Напомним, что шифртекст имеет вид
C = m(m + B) (mod N).
поэтому
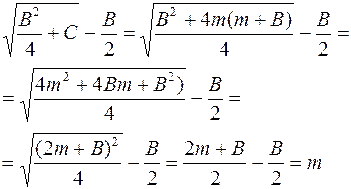
Конечно предполагаем, что мы выбрали правильный корень из четырех.
Пример. Открытый и закрытый ключи имеют вид:
- p = 127, q = 131,
- N = 16637 и B = 12345.
Для шифрования сообщения m = 4410 вычисляем
C = m(m + B) (mod N) = 4633.
При обратной операции сначала находим
T = B2/4 + C (mod N) = 1500,
а затем извлекаем квадратные корни из T по модулю p и q:

После этого, применяя китайскую теорему об остатках к паре
±22 (mod p) и ±37 (mod q),
находим квадратный корень из T по модулю N:

Четыре варианта расшифрования
4410, 5851, 15078, или 16519
получаются из формулы
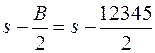 .
.
Дата добавления: 2016-02-13; просмотров: 3936;
