Рюкзачные криптосистемы.

Задача об укладке рюкзака. Задано множество {v_i} из k натуральных чисел и целое число S.

Требуется найти такое k-разрядное число n = (n_{k – 1}n_{k – 2}…n₁n₀)₂ (где n_i Î {0, 1} суть значения разрядов в двоичной записи чиcла n), что 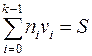, если такое n существует.

В зависимости от набора {v_i} и числа S, такого решения может не быть вообще, решений может быть несколько или решение будет единственным. Такая задача является сложной.

Частный случай – задача об укладке быстровозрастающего рюкзака. Это случай, когда величины v_i, будучи упорядочены в порядке возрастания, обладают тем свойством, что каждое число больше суммы всех предыдущих.

Такая задача имеет эффективный алгоритм решения:

1. Положим W = S и j = k.

2. Начиная с n_{j – 1} и последовательно уменьшая j, полагаем все n_j = 0 до тех пор, пока не придем к первому такому значению j (обозначим его через i₀), что 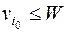. Положим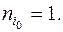

3. Заменим W на , положим j = i₀ и, если W > 0, то переходим к шагу 2.

4. Если W = 0, то цель достигнута. Если W > 0 и все оставшиеся v_i больше W, то ясно, что решения n = (n_{k – 1}n_{k – 2}…n₁n₀)₂ задачи не существует. Если решение есть, то оно единственное.

Пример. Набор {2, 3, 7, 15, 31} является быстрорастущим набором, а S = 24. Тогда проходя пятерку значений справа налево, мы видим, что n₄ = 0 (31 > 24), n₃ = 1 (15 < 24 и в этот момент заменяем 24 на 24 – 15 = 9), n₂ = 1 (7 < 9 и в этот момент заменяем 9 на 9 – 7 = 2), n₁ = 0 (3 > 2), n₀ = 1 (2 = 2). Таким образом, получаем n = (01101)₂ = 13.