Слабые моменты реализации RSA.

Разделенный модуль: Поскольку арифметика остатков – дорогое удовольствие с точки зрения компьютера, весьма заманчиво разработать систему шифрования, в которой пользователи разделяют общий модуль N, но применяют различные открытые и закрытые экспоненты (E_i, d_i).

Одна из причин, побуждающая это делать, - ускорить алгоритмы зашифрования и расшифрования в аппаратных средствах, специально настроенных на определенный модуль N. Однако это неудачная идея, поскольку пасует перед двумя типами нападающих: внутреннего, то есть законного пользователя системы, и внешнего.

Предположим, что нападающим является один из законных клиентов криптосистемы, скажем пользователь номер 1. Он может найти значение секретной экспоненты пользователя 2 – d₂. Сначала он вычисляет p и q по известному ему d₁. Затем злоумышленник находит

j(N) = (p – 1)(q – 1) и, наконец, при помощи расширенного алгоритма Евклида раскрывает значение d₂ по формуле

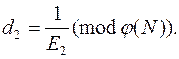
Предположим, что теперь атакующий не принадлежит к пользователям криптосистемы, использующей общий модуль. Допустим, происходит рассылка одинакового (допустим циркулярного) сообщения m двум клиентам криптосистемы, открытые ключи которых

(N, E₁) и (N, E₂).

Противник, нападающий извне, видит зашифрованные сообщения С₁ и C₂, где

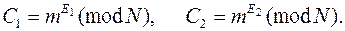
Он может вычислить

и восстановить сообщение m по следующей схеме:

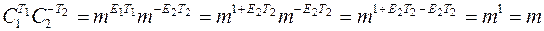
Пример. N = N₁ = N₂ = 18923, E₁ = 11 и E₂ = 5.

Предположим, что перехвачены шифртексты

C₁ = 1514 и C₂ = 8189,

соответствующие одному открытому тексту m. Тогда противник вычисляет T₁ = 1 и T₂ = 2, после чего раскрывает исходную информацию:

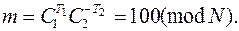
Вывод. При использовании общего модуля N любой законный пользователь системы может восстановить секретную экспоненту d другого пользователя, а внешний противник сможет читать циркулярные сообщения m.

Малые шифрующие экспоненты:

Иногда в криптосистемах RSA с целью экономии затрат на шифрование используются небольшие шифрующие экспоненты E. Это тоже создает дополнительные проблемы, связанные с криптостойкостью. Предположим, что есть три пользователя с различными модулями шифрования

N₁, N₂ и N₃

и одинаковой шифрующей экспонентой E = 3. Пусть некто посылает им одно сообщение m, зашифрованное тремя разными открытыми ключами. Нападающий видит три криптограммы:

C₁ = m³ (mod N₁),

C₂ = m³ (mod N₂),

C₃ = m³ (mod N₃)

и с помощью китайской теоремы об остатках находит решение системы

{X = C_i (mod N_i)| i = 1, 2, 3}

в виде

X = m³ (mod N₁N₂N₃).

Но поскольку m³ < N₁N₂N₃, целые числа X и m³ должны совпадать. Поэтому, вычисляя обычный кубический корень из X, нападающий раскрывает сообщение m.

Пример.

N₁ = 323, N₂ = 299, N₃ = 341

и перехваченные сообщения

C₁ = 50, C₂ = 299, C₃ = 1,

Чтобы восстановить исходное сообщение m, находим решение системы

X = 300763 (mod N₁N₂N₃),

после чего извлекаем обычный кубический корень

m = X^1/3 = 67.

Вывод. При использовании малой шифрующей экспоненты E противник может восстановить циркулярное сообщение m для E пользователей.

Обе вышеуказанные атаки позволяют раскрыть текст, не прибегая к разложению на множители. Наиболее важный вывод из них – необходимость дополнять оригинальные сообщения случайными цифрами перед их зашифрованием.

При практической реализации RSA необходимо решить следующие задачи:

1. Генерация больших простых чисел p и q с проверкой выполнения соответствующих требований к ним.

2. Выбор экспонент e и d с соблюдением соответствующих требований.

3. Реализация операции вычисления x^y(mod n).

Генерация большого простого числа:

1) Сгенерировать случайное n-битовое число p.

2) Установить старший и младший бит равными 1. (Старший бит гарантирует требуемую длину простого числа, а младший – обеспечивает его нечетность).

3) Убедиться, что p не делится на малые простые числа: 3, 5, 7, 11 и т.д. Во многих практических реализациях проверяется делимость p на все простые числа, меньшие 256. Наиболее надежна проверка делимости на все простые числа, меньшие 2000. Эти проверки можно выполнить на основе массива этих простых чисел.

4) Выполнить тест простоты Рабина-Миллера для некоторого случайного числа a. Если p проходит тест, сгенерировать другое случайное число a и повторить тест. Для ускорения проверки можно выбирать относительно небольшие значения a. Выполнить тест минимум пять раз. Если p не проходит один из тестов, то перейти к шагу 1).

Другой путь – не генерировать случайное число p в каждом тесте, а последовательно перебирать все нечетные числа, начиная со случайно выбранного числа, пока не найдется простое число.

Тест Рабина-Миллера:

Выбрать для тестирования число p. Вычислить b – число делений p – 1 на 2 (то есть 2^b – это наибольшая степень числа 2, на которую делится p – 1). Затем вычислить m, такое, что p = 1 + 2^b · m.

1) Выбрать случайное число a, меньшее p.

2) Установить j = 0 и z = a^m mod p.

3) Если z = 1 или если z = p – 1, то p проходит тест и может быть простым числом.

4) Если j > 0 и z = 1, то p не относится к простым числам.

5) Установить j = j + 1. Если j < b и z ¹ (p – 1), установить z = z² mod p и вернуться к шагу 4). Если z = p – 1, то p проходит тестирование и может быть простым числом.

6) Если j = b и z ¹ (p – 1), то p не относится к простым числам.

Выбор экспонент e и d:

1) Так как единственное требование к e – отсутствие общих множителей с числом φ(n) = (p - 1) · (q - 1), то логично выбирать небольшое e легко разложимое на простые множители и осуществлять проверку делением φ(n) на множители e. Либо выбирать простое e. Неплохо также выбирать e с минимальным количеством единиц в двоичном представлении, что ускорит операцию возведения в степень, реализованную следующим алгоритмом.

2) Так как очевидно, что d = e^-1(mod p), то d находим при помощи расширенного алгоритма Евклида.

Алгоритм вычисления x^y(mod n).

1) Представим y в двоичной системе счисления y = y₀2^r + … + y_r-12 + y_r, где y_i, цифры в двоичном представлении равные 0 или 1, y₀ = 1.

2) Положим x₀ = x и затем для i = 1,…, r вычислим

.

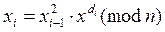3) x_r есть искомый вычет x^y(mod n).