Взаимосвязь компонентов RSA.
Задача RSA: Даны числа C и E, последнее из которых удовлетворяет соотношению:
НОД(E, (p – 1)(q – 1)) = 1.
Требуется найти такое число m, что
mE = C (mod N).
Лемма. Задача RSA не сложнее проблемы факторизации.
Доказательство. Применяя алгоритм факторизации, разложим число N на простые множители, вычислим значение функции Эйлера Ф = j(N) и найдем
D = 1/E (mod Ф).
Теперь, зная число D, легко восстановить m, поскольку
CD = mED = m1 (mod Ф) = m (mod N).
Отсюда следует, что при известных p и q легко находятся d и m.
Самые большие числа, которые к настоящему времени удается разложить на множители за разумное время, имеют 500 двоичных знаков. В связи с этим, для обеспечения стойкости систем среднего срока действия, рекомендуют брать модули шифрования порядка 1024 бит. Для систем большого срока действия следует выбирать модули, состоящие из 2048 бит.
Секретная экспонента и проблема факторизации:
Лемма. Если известна секретная экспонента d алгоритма RSA, соответствующая открытому ключу (N, E), то число N можно эффективно разложить на множители.
Доказательство. При некотором целом s имеет место равенство
Ed – s(p – 1)(q – 1) = 1.
Возьмем произвольное целое число X ¹ 0. Тогда
XEd – 1= 1(mod N).
Вычисляем квадратный корень Y1 по модулю N:
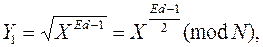
что можно сделать, поскольку Ed – 1 известно и четно. Приходим к тождеству
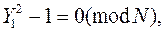
которое можно использовать для определения делителей числа N с помощью вычисления НОД(Y1 – 1, N). Однако это будет работать только если Y1 ¹ ±1 (mod N).
Предположим, что нам не повезло и Y1 = ±1 (mod N). Если Y1 = –1 (mod N), вернемся к началу и выберем другое число X. Если Y1 = 1 (mod N), то можно взять еще один квадратный корень
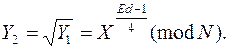
Опять получаем
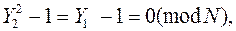
откуда НОД(Y2 – 1, N) – делитель числа N. К сожалению, здесь тоже может оказаться, что Y2 = ±1 (mod N). Тогда придется повторить все снова.
Алгоритм необходимо повторять до тех пор, пока мы не разложим N на множители и не придем к числу (ED – 1)/2t, которое уже не будет делиться на 2. В последнем случае придется вернуться к началу алгоритма, выбрать новое случайное значение X и все повторить.
Отсюда следует, что при известном d легко найти p и q.
Алгоритм, приведенный в доказательстве, - типичный пример алгоритма Лас-Вегаса, вероятностного по своей природе, которая проявляется в процессе работы. Но если уж ответ отыщется, то он будет обязательно верным.
Пример. Входные данные задачи RSA:
N = 1441499, E = 17 и d = 507905.
Напомним, что мы предполагаем известной расшифровывающую экспоненту d, которая обычно хранится в секрете. Опираясь на предыдущий алгоритм, найдем числа N. Положим
T1 = (Ed – 1)/2 = 4317192,
X = 2.
Для вычисления Y1, сделаем преобразования :
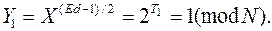
Поскольку Y1 оказался равным 1, нам нужно взять
T2 = T1/2 = (Ed – 1)/4 = 2158596 и 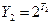 .
.
Теперь
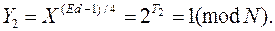
Снова нужно повторять предыдущие шаги, что приведет нас к
T3 = (Ed – 1)/8 = 1079298
и
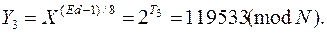
Отсюда
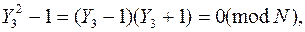
и мы можем найти простой делитель числа N, вычислив
НОД(Y3 – 1, N) = 1423.
Значение функции Эйлера j(N) и проблема факторизации:
Лемма. Значение Ф = j(N) позволяет эффективно разложить число N на множители.
Доказательство. Имеем
Ф = (p – 1)(q – 1) = N – (p + q) + 1.
Следовательно, положив S = N + 1 – Ф, мы получим
S = p + q.
Нам нужно определить числа p или q, опираясь на их сумму S и произведение N. Рассмотрим многочлен
f(X) = (X – p)(X – q) = X2 – SX + N.
Теперь можно найти как p, так и q, решая квадратное уравнение f(X) = 0 стандартным образом:
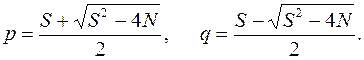
Отсюда следует, что при известном j(N) легко найти p и q.
Пример. Открытый модуль N = 18923 криптосистемы RSA. Известно Ф = j(N) = 18648. Вычисляем
S = p + q = N + 1 – Ф = 276.
Соответствующий многочлен имеет вид:
f(X) = X2 – SX + N = X2 – 276X + 18923,
а его корни – p = 149, q = 127.
Дата добавления: 2016-02-13; просмотров: 1547;
