Алгоритм цифровой подписи Эль-Гамаля.

Схема цифровой подписи Эль-Гамаля основана на сложности вычисления дискретных логарифмов в конечном поле.

Так же как и для шифрования Эль-Гамаля выбираются параметры системы:

P – большое простое число (порядка 1024-2048 бит).

Q – простой делитель числа P – 1 (порядка 160 бит).

G – порождающий элемент мультипликативной группы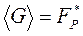

Секретным ключом является:

x – целое случайное число в диапазоне 2 ≤ x ≤ P – 2.

Открытый ключ Y вычисляется по формуле:

Y = G^x (mod P).

Подпись для сообщения M вычисляется при помощи следующего алгоритма:

1. Выбрать случайный эфемерный сеансовый ключ k, 2 ≤ k ≤ P – 2, взаимно простой с P – 1, НОД(k, P – 1) = 1.

2. Вычислить R = G^k (mod P).

3. Вычислить S = (M - xR)k ^-1 (mod P – 1).

4. Подписью сообщения M служит пара (R, S).

Если сообщениe M большое, то при вычислении S используют его хэш-значение H(M).

Алгоритм проверки подписи заключается в проверке сравнения:

.

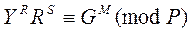Основным достоинством данной схемы является возможность выработки цифровых подписей для большого числа сообщений с использованием одного секретного ключа.

Пример. Выберем P = 11 и G = 2, а закрытый ключ x = 8.

Вычислим

Y = G^x mod P = 2⁸ mod 11 = 3.

Открытым ключом являются Y = 3, G = 2, и P = 11. Чтобы подписать M = 5, сначала выберем случайное k = 9. Убеждаемся, что НОД(9, 10) = 1. Вычисляем:

R = G^k mod P = 2⁹ mod 11 = 6.

Далее с помощью расширенного алгоритма Евклида находим k ^{– 1} = 9 mod (11 – 1) и S:

S = (M - xR)k ^-1 (mod P – 1) = (5 – 8 · 6) · 9 mod (11 – 1) = 3.

Подпись составит пару (6, 3).

Для проверки подписи убедимся что:

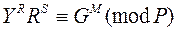
3⁶·6³ mod 11 = 2⁵ mod 11.

Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи. В их основе лежит проверка сравнения вида:

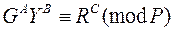
в котором тройка (A, B, C) совпадает с одной из перестановок чисел ±M, ±S, ±R.

Например, исходная схема Эль-Гамаля получается при

A = M, B = – R и C = S.

Еще одно достоинство данного семейства является возможность уменьшения длины подписи путем замены пары чисел (R, S) на пару чисел (R mod Q, S mod Q). При этом проверочное равенство по модулю P следует заменить на модифицированное равенство по модулю Q:

.

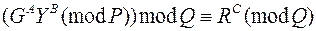На основе семейства данных схем построены стандарты цифровой подписи DSS и ГОСТ Р34.10-94.

Кроме того, данное семейство может быть модифицировано для работы с группой точек эллиптической кривой.