Схема с дополнением на основе RSA.

Предположим, дано длинное сообщение M для визирования. Сначала вычисляется H(M) и потом применяется преобразование подписи RSA к хэш-свертке H(M), то есть подпись получается так:

S = (H(M))^d (mod N).

Наконец, подпись и само сообщение передаются вместе в виде пары (M, S).

Проверка пары (M, S) состоит из трех этапов:

- «Зашифрование» S с помощью открытой экспоненты RSA для получения H’:

H’(M) = S^E (mod N).

- Вычисление H(M) по M.

- Проверка равенства H’(M) = H(M). Если оно верно, то подпись законна. В противном случае – незаконна.

5.2.3. Алгоритм цифровой подписи Фиата – Фейге – Шамира.

Алгоритм основан на сложности задач факторизации больших целых чисел и извлечения квадратного корня в кольце вычетов. В данном алгоритме реализуется цифровая подпись с дополнением.

Пусть H – некоторая хэш-функция, преобразующая исходное сообщение в битовую строку длины m. Выбирают два простых числа p и q и вычисляют N = p · q. В качестве секретного ключа каждый абонент должен сгенерировать m различных случайных чисел a₁,a₂,...,a_m Î Z_N. Открытым ключом объявляется набор чисел B₁,B₂,...,B_m Î Z_N, где

Алгоритм вычисления цифровой подписи для сообщения M состоит в выполнении следующих действий:

1. Выбрать случайное число r, 1 < r < N – 1.

2. Вычислить u = r² mod N.

3. Вычислить H(M, u) = S = (S₁,S₂,...,S_m).

4. Вычислить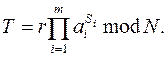

5. Подписью для M положить пару (S, T).

Алгоритм проверки подписи состоит в выполнении следующих действий:

1. По открытому ключу B₁,B₂,...,B_m mod N и значению T вычислить

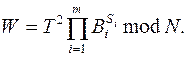
2. Вычислить H(M, W) = S’.

3. Проверить равенство S = S’.

Достоинствами описанной схемы являются возможность выработки цифровых подписей для нескольких различных сообщений с использованием одного секретного ключ, а также сравнительная простота алгоритмов вычисления и проверки подписи. Попытка компрометации данной схемы сталкивается с необходимостью решения сложной задачи нахождения квадратных корней по модулю N. Недостатком схемы является большая длина ключа, которая определяется числом m. если двоичная запись числа N содержит l знаков, то длина закрытого ключа составляет ml бит, а открытого ключа – (m + 1)l бит. При этом необходимо учитывать, что для обеспечения достаточной стойкости данной схемы цифровой подписи числа m и l должны иметь в своей двоичной записи несколько сотен бит.

Пример. Если p = 5, q = 7, N = 35, то возможными квадратичными вычетами являются:

1: x² º 1 (mod 35) имеет решения: x = 1, 6, 29, 34.

4: x² º 1 (mod 35) имеет решения: x = 2, 12, 23, 33.

9: x² º 1 (mod 35) имеет решения: x = 3, 17, 18, 32.

11: x² º 1 (mod 35) имеет решения: x = 9, 16, 19, 26.

14: x² º 1 (mod 35) имеет решения: x = 7, 28.

15: x² º 1 (mod 35) имеет решения: x = 15, 20.

16: x² º 1 (mod 35) имеет решения: x = 4, 11, 24, 31.

21: x² º 1 (mod 35) имеет решения: x = 14, 21.

25: x² º 1 (mod 35) имеет решения: x = 5, 30.

29: x² º 1 (mod 35) имеет решения: x = 8, 13, 22, 27.

30: x² º 1 (mod 35) имеет решения: x = 10, 25.

Обратными значениями (mod 35) и их квадратными корнями являются

Обратите внимание, что у чисел 14, 15, 21, 25 и 30 нет обратных значений по модулю 35, так как они не взаимно простые с 35. Это верно, так как должно быть

(p – 1)(q – 1)/4 = (5 – 1)(7 – 1)/4 = 6

квадратичных вычетов по модулю 35, взаимно простых с 35. Поэтому НОД(x, 35)должен быть равен 1.

Для хэш-функции H со сверткой длины m = 4 выберем открытый ключ

{B_i } = {4, 11, 16, 29};

и соответственно закрытый ключ

{a_i } = {3, 4, 9, 8}.

Выбираем r = 16, вычисляем u = r² = 16² mod 35 = 11.

Допустим значение хэш-свертки сообщения M и u составило:

S = H(M, u) = (1, 1, 0, 1).

Вычисляем

T = 16 · (3¹ · 4¹· 9⁰· 8¹) (mod 35) = 31

При проверке подписи вычисляют

W = 31² · ( 4¹· 11¹· 16⁰· 29¹) (mod 35) = 11 = u.

Но так как проверяющий не знает u, то он для проверки вычисляет хэш-свертку

S’ = H(M, W) = (1, 1, 0, 1) = S.