Алгоритм цифровой подписи DSA.

Рассмотрим данный алгоритм более подробно, так как на его основе построен стандарт цифровой подписи DSS. DSA – алгоритм подписи с дополнением в котором собственно подпись состоит из двух 160-битовых целых чисел R и S. Число R является функцией 160-разрядного случайного числа k, которое называют эфемерным ключом, изменяемым с каждым новым сообщением. Число S – функция от сообщения, секретного ключа x, принадлежащего подписывающему лицу, числа R и эфемерного ключа k. Аналогисно алгоритму Эль-Гамаля здесь есть несколько параметров домена. Для из задания сначала фиксируется 160-битовое простое число Q, а затем выбирается такое большое простое число P, лежащее между 2⁵¹² и 2²⁰⁴⁸, что P – 1 делится на Q. Наконец генерируется случайное число H < P и вычисляется

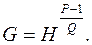
Если G = 1, то переходят к другому случайному H до тех пор, пока не получат G ¹ 1.

Этим обеспечивается выполнение следующего условия: G – порождающий элемент группы 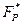порядка Q, то есть

G^Q = 1 (mod P).

После выбора параметров домена (P, Q, G) каждый пользователь генерирует свой собственный закрытый подписывающий ключ x, удовлетворяющий неравенству 0 < x < Q. Соответствующим открытым ключом служит число Y, вычисляемое по правилу

Y = G^x (mod P).

Процедура выбора пользовательской ключевой пары существенно проще, чем в RSA, поскольку она требует всего лишь одного возведения в степень в числовом поле.

Подписание сообщения осуществляется по следующему алгоритму:

- вычисляют значение хэш-функции H = H(M),

- выбирают случайный эфемерный ключ k, 0 < k < Q,

- определяют R = (G^k (mod P)) (mod Q),

- находят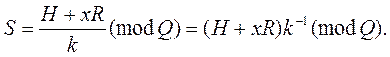

Подписью сообщения M служит пара (R, S), имеющая в общей сложности 320 двоичных знаков.

Для проверки подписи (R, S) на сообщении M делают так:

- вычисляют значение хэш-функции H = H(M),

- определяют A = H/S (mod Q) и B = R/S (mod Q),

- находят

V = (G^AY^B (mod P))(mod Q),

где Y – открытый ключ автора сообщения.

- Подпись считается корректной только тогда, когда V = R.

Пример. Параметры домена Q = 13, P = 4Q + 1 = 53 и G = 16.

Предположим, что ключевая пара имеет вид x = 3 и Y = G^x (mod P) = 16³ (mod 53) = 15. Если мы хотим подписать сообщение с хэш-значением H = 5, то сначала нужно выбрать эфемерный ключ k = 2 и найти

R = (G^k (mod P)) (mod Q) = (16² (mod 53))(mod 13) = 44 mod 13 = 5,

S = (H + xR)/k (mod Q) = (5 + 3 · 5) · 2^-1 (mod 13) = (5 + 3 · 5) · 7 (mod 13) = 10.

Для проверки подписи получатель определяет

A = H/S (mod Q) = 5 · 10^-1 (mod 13) = 5 · 4 = 7,

B = R/S (mod Q) = 5 · 10^-1 (mod 13) = 7,

V = (G^AY^B (mod P))(mod Q) = (16⁷ · 15⁷ (mod 53)) (mod 13) = (49 · 42 (mod 53))(mod 13) = 5.

Ввиду равенства V = R = 5 делаем вывод о корректности подписи.