Формирование огибающей спектра последовательности прямоугольных видеоимпульсов

Рассмотрим процессы, возникающие в последовательном колебательном контуре с высокой добротностью Q>>1 при воздействии на него периодической последовательности прямоугольных видеоимпульсов с амплитудой U длительностью τ и периодом T = 1/F =2p/W (рис. 4.32). Контур используется здесь в качестве последовательного анализатора спектра с перестраиваемой частотой ω₀=2pf₀=2p/T₀. Благодаря высокой добротности контура потери энергии в нем будут очень малы и за время, сравнимое с длительностью периода T, амплитуда его собственных колебаний практически не изменится. Это позволяет нам рассматривать его на таком отрезке времени как контур без потерь.

Выше, в разделе 4.7, мы уже рассматривали воздействие такой последовательности видеоимпульсов на контур. Однако там было принято условие τ<<Т₀,при выполнении которого видеоимпульс воспринимается контуром как однократный электрический "щелчок". В общем же случае, когда τ~Т₀ и, особенно, при τ>>Т₀ необходимо учитывать раздельное воздействие на контур как переднего, так и заднего фронтов видеоимпульса.

На контур сначала приходит передний фронт импульса, который представляет собой скачек напряжения с амплитудой U. Что бы найти ток, возникающий в этом случае в контуре, необходимо решить дифференциальное уравнение этого контура с правой частью:

.

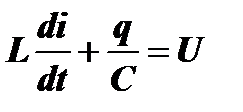Начальные условия в контуре при t=0 в этом случае будут нулевыми: i=0 и q=0. Закон изменения тока в контуре, полученный в результате решения этого уравнения, будет таким же, как и для контура, в котором при t=0 заряженный конденсатор разряжался через индуктивность (раздел 4.4):

,

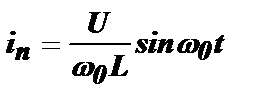где 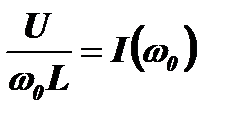– амплитуда тока в контуре;

Отметим, что амплитуда тока I(ω₀) имеет обратную зависимость от частоты контура ω₀. В результате с увеличением частоты контура эта амплитуда уменьшается по гиперболическому закону.

Теперь учтем воздействие на контур заднего фронта импульса. Этот фронт вызовет в контуре аналогичный ток, только отстающий по времени на длительность импульса t и поэтому имеющий сдвиг по фазе на φ_τ=ω₀t. В отличие от тока, возбужденного передним фронтом, который имеет положительную производную и начинается с положительной полуволны, ток, возбужденный задним фронтом, имеет отрицательную производную и начинается с отрицательной полуволны. В результате начальные фазы этих токов отличаются на 180^о, а выражение для тока i_з имеет вид:

.

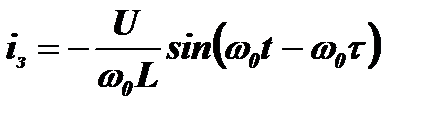Суммарный ток, оставшийся в контуре после окончания импульса, можно записать следующим образом:

.

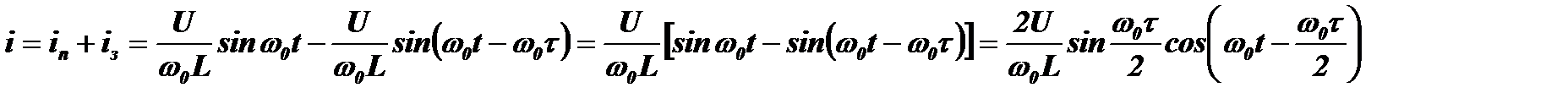В результате сложения двух токов суммарная амплитуда тока в контуре:

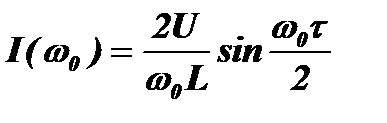
получает дополнительный периодический множитель, который зависит от частоты контура w₀и длительности импульса t: Умножив и разделив это выражение на t, получим зависимость амплитуды суммарного тока от частоты:

,

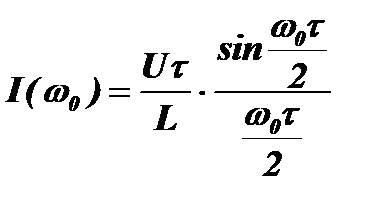которая является огибающей физического спектра и так же, как и огибающая математического спектра, изменяется по закону 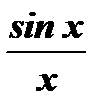.Подставляя в это выражение вместо частоты w₀ в это выражение частоту частоты гармоник спектра nw, можно получить их амплитудные значения I(nw).

При определении амплитуды на частоте w₀=0(постоянная составляющая спектра), в выражении для I(w₀) возникает неопределенность типа 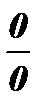. Раскрывая ее по правилу Лопиталя, получим:

.

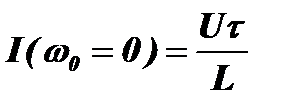При настройке контура на частоты, близкие к нулевым, ёмкость контура заряжается от внешнего импульса также, как и на более высоких частотах. Однако колебательный процесс в контуре до прихода следующего импульса практически не возникает, так как период колебаний контура на этих частотах Т_о>>Т. В результате каждый следующий импульс вносит в ёмкость контура дополнительный заряд и напряжение на ней постепенно растет. В контуре, имеющем очень малые потери, амплитуда этого напряжения будет расти, пока не станет равной амплитуде импульсов, воздействующих на контур. Это и будет постоянная составляющая физического спектра.