АНАЛИЗАТОРЫ СПЕКТРА

Предисловие

Цепи и сигналы – два аспекта передачи и преобразования информации в тракте любого радиотехнического устройства, каждый из них не имеет смысл без другого. Поэтому два главных аппаратных исследования, связанных с этими передачей и преобразованием – анализ цепей и анализ сигналов. Число параметров и характеристик сигналов, интересных для практики и теории, бесконечно. Очевидно, первое (но не единственное!), с чего нужно начинать анализ сигналов, это спектральный анализ – при характеризации в частотной области, и форма сигнала – при характеризации во временной области.

Фактически спектральный анализ электромагнитных колебаний восходит к 17 веку, когда был открыт спектральный прибор – призма, реагирующий на частоту света, и начало изучаться и использоваться спектральное разложение света призмой. Еще раньше производились генерация и анализ спектральных составляющих звука на базе таких спектральных приборов, как струна, мембрана, воздушный резонатор. Однако переход к осознанному количественному спектральному анализу стал возможен только с работ Ж.-Б.Ж. Фурье, фактически открывшего спектрально-временной дуализм прикладных функций. С появлением радиотехники сразу возникла необходимость анализа сигналов, в частности, спектрального анализа. В качестве спектрального прибора использовался резонатор, в качестве вспомогательных явлений – интерференция и преломление в диспергирующей среде. Из двух принципиальных разновидностей аппаратного спектрального анализа – параллельного и последовательного действия – в универсальных спектроанализаторах выжила вторая, в то время как для специализированных часто используется первая.

Главной особенностью задачи спектрального анализа сигналов СВЧ является чрезвычайное разнообразие структур сигналов, используемых в различных радиоэлектронных приложениях, и разнообразие значений их параметров. Это чрезвычайно усложняет структуру, архитектуру и функциональную вариативность спектроанализатора, имеющего претензии на универсальность. Такие параметры прибора, как ширина обозреваемой частотной области, шаг частотной дискретизации, частотное разрешение, степень видеоусреднения, степень сглаживания измеряемых характеристик и др. должны иметь возможность варьировать при установке в очень широких пределах.

К настоящему времени спектроанализаторы СВЧ стали важнейшим измерительным и индицирующим средством характеризации высокочастотных и сверхвысокочастотных сигналов самой разнообразной структуры. Современный универсальный спектроанализатор ВЧ и СВЧ относится к четвертому поколению радиоизмерительных приборов; позволяет вести автоматическую регистрацию амплитудных (скалярный анализатор) и комплексных (векторный анализатор) спектров панорамно по частоте, вплоть до рабочей полосы 0–110 ГГц; в большой мере управляется и вычислительно обслуживается внутренним или внешним компьютером; использует как минимум тройное преобразование частоты, гетеродины которого построены на высокостабильных синтезаторах частоты; широко использует цифровые технологии, в частности, имеет полностью цифровой тракт, начиная с выхода последнего смесителя; автоматически представляет и сохраняет спектральные характеристики сигналов в различных форматах, масштабах и подробностях; может быть включен в систему метрологического трассирования вплоть до национальных стандартов.

Тем не менее, возможности увеличения эффективности векторных и скалярных спектроанализаторов далеко не исчерпаны. Косвенным свидетельством этому является ежегодное появление на рынке измерительных приборов СВЧ все новых, более совершенных моделей анализаторов ведущих мировых фирм. Можно предположить, что в связке с технологическими прорывами радиотехнического значения и рыночной коньюнктурой основными направлениями развития будут:

1) дальнейшая виртуализация системы, то есть передача выполняемых функций от радиотехнических устройств к компьютерам;

2) совершенствование системы измерительных калибровок;

3) дальнейшая автоматизация цикла измерений, вплоть до почти полного устранения ручных операций;

4) совершенствование системы интерпретации наблюдаемых данных на базе специально разработанной теории интерпретации спектрометрических данных;

5) дистанционное управление работой прибора;

6) расширение возможностей включения прибора в измерительный комплекс без доработки интерфейсов и т.п.

Теоретические предпосылки

Цель аппаратного спектрального анализа

Будем пока для простоты считать сигнал действительной конечной непрерывной функцией времени. Фактически при изложении на названном уровне обычно предполагается (явно или неявно), что сигнал детерминированный (в смысле – не случайный), то есть найденная аппаратно спектральная характеристика интерпретируется как характеристика данного сигнала, а не оценка характеристики некоторой совокупности реализаций (ансамбля) случайного процесса, полученная по одной реализации. Впрочем, предположение о детерминированности сигнала не сужает дальнейших технических возможностей, т.к. названная оценка легко получается из спектральной характеристики детерминированного сигнала.

Итак, в свете сделанных оговорок будем считать, что целью скалярного аппаратного спектрального анализа является получение амплитудного спектра (амплитудной спектральной плотности) 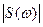сигнала 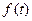, а целью векторного аппаратного спектрального анализа является получение комплексного спектра (комплексной спектральной плотности) 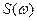. Здесь комплексный спектр определен как преобразование Фурье (интеграл Фурье) от сигнала:

,

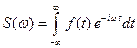а амплитудный спектр – как модуль комплексного спектра.

В свою очередь, при определенных условиях (всегда выполняющихся при сделанных предположениях) сигнал как временная функция может быть получен из комплексного спектра (но не амплитудного!) обратным преобразованием Фурье:

.

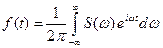Говорят, что в виде 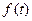сигнал представлен во временной области, а в виде 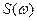– в частотной области. Амплитудный спектр суть неполное представление сигнала в частотной области, именно поэтому, зная только его, невозможно восстановить 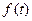. Это обстоятельство – один из главных стимулов для создания гораздо более сложных векторных спектроанализаторов (иногда – на опциональной основе).

Используя экспоненциальную форму комплексного числа 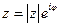, запишем комплексный спектр в виде

.

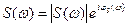Как видим, комплексный спектр характеризуется двумя функциями: амплитудным спектром 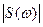и фазовым спектром 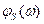. Сделаем два замечания.

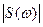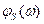1) Как и при любом аппаратурном измерении, функции и находятся с ошибками (случайными и систематическими), меры которых сами являются функциями частоты 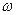; то есть на самом деле мы получаем статистические оценки 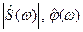искомых функций. Частотные функции мер ошибок зависят как от специфических свойств спектральных оценок [2.1], так и структуры спектроанализатора и его обработки сигналов. Если первым зависимостям посвящены многочисленные работы (в основном, на общетеоретическом уровне), то исследование вторых представляет обширное поле для деятельности, частично освоенное на частном, утилитарном уровне.

2) Если представление сигнала во временной области получается обратным преобразованием Фурье из 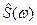(а не непосредственной его записью), то и это представление есть оценка 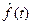временной функции; временные функции мер ошибок этой оценки связаны непростыми зависимостями с частотными функциями мер ошибок спектральных оценок (плюс ошибки численного расчета обратного преобразования Фурье).

Параллельный и последовательный анализ

Для целей аппаратного спектрального анализа необходим спектральный прибор, реагирующий на частоту колебаний. Поиск рабочих физических эффектов для создания спектральных приборов шел с 17 века, когда было открыто и начало использоваться спектральное разложение света призмой. Тем не менее, и в середине двадцатого века можно было всего лишь констатировать, что «в основе действия спектральных приборов лежит одно из следующих явлений: интерференция, преломление при наличии дисперсии, резонанс» [2.2]. В радиотехнике, в том числе на СВЧ давно победили методы спектрального анализа с помощью резонанса, то есть с использованием резонаторов.

Существует две принципиальные возможности аппаратного спектрального анализа с помощью резонаторов. Первый способ состоит в применении набора резонаторов, настроенных на различные частоты и подвергающихся одновременно воздействию исследуемого колебания; этот способ называется одновременным (параллельным) анализом. Второй способ предполагает применение одного резонатора с переменной настройкой (модификацию этого способа мы рассмотрим ниже); этот способ называется последовательным анализом.

На первый взгляд, параллельный анализ имеет ряд преимуществ перед последовательным. Во-первых, кажется очевидным, что параллельный анализ более быстрый, т.к. скорость перестройки резонатора в последовательном анализе ограничена искажениями, создаваемыми переходными процессами. Во-вторых, последовательный анализ кажется малопригодным при быстро протекающих, быстро изменяющихся, нестационарных процессах. В-третьих, кажутся трудными и малоэффективными процессы калибровки считывания настройки резонатора в каждый момент времени.

Однако, логика технического прогресса в данной области привела к почти полной победе последовательного анализа, по крайней мере, в универсальных спектроанализаторах (правда, после некоторой модификации), оставившего параллельному анализу только исключительные, редкие ситуации: спонтанные, непрогнозируемые, неповторяющиеся СВЧ-«вспышки» и т.п. Решающими факторами этой «победы» оказались гибкость, автоматизируемость и точность анализа.

Упомянутая модификация последовательного анализа состоит в том, что вместо плавной управляемой перестройки резонатора используется управляемый сдвиг спектра самого сигнала во времени. Это стало возможным благодаря применению супергетеродинирования, в результате которого селективные функции отделены от функций перестройки и выполняются на постоянной промежуточной частоте, что обеспечивает возможность прецизионного регулирования параметров частотной селекции (полосы, крутизны среза и т.п.). В технике спектрального анализа супергетеродинный принцип сыграл столь же революционную роль, как и вообще в технике перестраиваемого приема сигналов.

На самом деле, техническое совершенствование как параллельного, так и последовательного анализа не является стратегической целью построения совершенного спектроанализатора будущего, именно потому, что эти методы опосредованы свойствами резонансной системы. Чтобы понять, к чему следует стремиться в аппаратном анализе сигнала, как ни парадоксально, необходимо отказаться от первого же утверждения, с которого мы начали данное изложение: что «… необходим спектральный прибор …». Действительно, как будет показано ниже, спектральный прибор, будь то резонатор или другая система, принципиально вносит свои искажения в получаемый продукт, отличающийся от желаемого спектра сигнала; более того, эти искажения бывает трудно учесть.

Стратегическая цель развития аппаратного анализа спектра должна основываться на непосредственной записи сигнала и выполнении численного преобразования Фурье от него (здесь мы для простоты обсуждения предполагаем детерминированный сигнал; спектральный анализ случайного сигнала будет рассмотрен позже). На языке сегодняшней цифровой техники сказанное означает оцифровку сигнала уже на сверхвысоких частотах и выполнение быстрого преобразования Фурье (БПФ) от него. Достижение этой цели сдерживается лишь недостаточной скоростью АЦП. Например, приняв достаточным период отсчетов в 6 градусов фазы, потребуем 60 отсчетов на периоде синусоиды, что на частоте 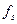сигнала требует скорости АЦП 60 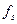отсчетов в секунду (о/с). При частоте 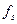=1 ГГц это означает 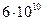о/с, при частоте 10 ГГц – 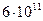о/с и т.д. Ясно, что применительно к интересующему нас диапазону СВЧ такие скорости лежат далеко за пределами возможностей современных АЦП. Этот вывод не изменится, если мы ограничимся всего лишь 20 отсчетами на периоде синусоиды. Более того, достижение скоростей в 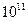– 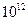о/c и более, по-видимому, потребует изменений структурных элементов АЦП на технологическом уровне. В настоящее время оцифровка сигнала (с последующей цифровой обработкой) производится лишь в тракте последней промежуточной частоты, так что предыдущие аналоговые элементы фильтрации вносят свою лепту в искажения получаемой спектральной характеристики.

Текущий спектр

Пусть бесконечный по длительности сигнал воспринимается спектроанализатором по мере поступления и обрабатывается в реальном или почти реальном времени. В этих условиях вычисление прямого преобразования Фурье в бесконечных пределах невозможно по двум причинам: во-первых, сигнал 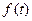поступает на систему обработки лишь с некоторого конечного момента времени 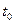; во-вторых, он известен (поступал) лишь до текущего момента 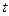. Приняв момент 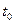за начало отсчета времени, мы констатируем, что в качестве спектральной характеристики сигнала вынуждены взять функцию частоты, задаваемую усеченным интегралом Фурье:

.

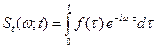Функция частоты 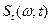, параметрически зависящая от времени 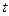, называется текущим спектром сигнала .

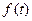Введение этого понятия учитывает один из важнейших аспектов реального измерения и уточняет цель аппаратного спектрального анализа сигнала: этой целью не может быть получение «истинного» спектра 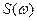; максимум, на что можно рассчитывать, это текущий спектр 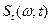. В связи с этим возникает ряд вопросов: при каких условиях и в каком смысле текущий спектр 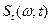сходится при 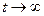к «истинному» спектру 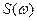? Какова скорость этой сходимости? Какова оценка ошибки текущего спектра 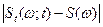как функции времени? Рассмотрение этих вопросов увело бы нас далеко в сторону от цели данной главы. Рассмотрим лишь простой пример.

Пусть сигнал имеет вид 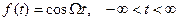. «Истинный» спектр (см. 3.10):

.

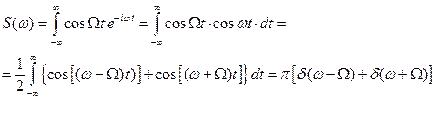Для удобства перехода к пределу и избавления от мнимой части, текущий спектр вычислим, поместив начало отсчета времени в середине интервала наблюдения сигнала:

.

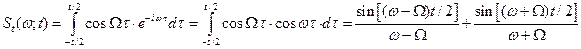Нетрудно найти, что при .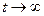

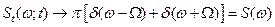До сих пор предполагался общий случай существования сигнала на всей оси времени (возможно, с убыванием на 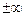). В частном случае сигнал финитен, то есть отличен от нуля на некотором конечном интервале времени 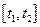. Тогда, если спектроанализатор был готов принимать и обрабатывать сигнал до момента 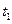и делал это до момента 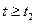, текущий спектр 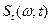к моменту 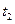совпал с «истинным» спектром 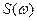, а дальнейшее измерение его не изменило. Если сигнал финитен, но очень длительный, для выполнения этих условий потребуется отказаться от требования обработки в реальном или почти реальном времени.

Мгновенный спектр