Виртуальная модель обработки сигнала при последовательном анализе

Пусть каждый фильтр модели (то есть фильтр ПЧ) построен на резонаторе низкого (например, первого) порядка, а входной сигнал содержит одну единственную спектральную линию на частоте 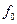, показанную на рис. 2.1.2а [2.2] вертикальной пунктирной линией. На этом рисунке показаны положения АЧХ фильтров модели, а пересечения пунктирной линии с кривыми показывают амплитуды отклика спектральной линии в разных фильтрах. Эти амплитуды можно привести к одной резонансной кривой, показанной на рис. 2.1.2б, поскольку их относительные значения (для фильтра первого порядка):

.

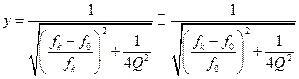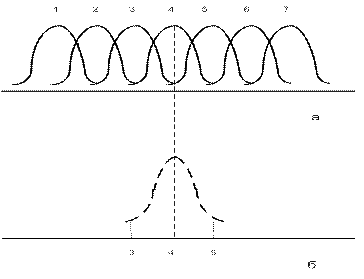
Таким образом, одна спектральная линия вызывает (разные по величине) отклики в нескольких фильтрах; идентифицировать линию можно по максимальному отклику. С увеличением 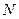(то есть уменьшением 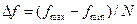) частотное расстояние между откликами уменьшается и при 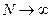спектральный отклик модели стремится к дискретному аналогу спектрального отклика рассмотренного выше последовательного анализа с непрерывной перестройкой фильтра. В реальных СА обычно 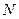очень велико, например, 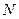=400. Поэтому с точностью до дискретизации откликов статическая разрешающая способность СА с дискретно-последовательным анализом та же, что для рассмотренного выше СА с медленной непрерывной перестройкой, то есть задается полосой разрешения

.

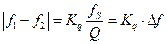Заметим теперь, что для СА с дискретно-последовательным анализом использование в тракте ПЧ фильтра на резонаторе низкого порядка еще более неоптимально, чем для гипотетического СА с плавной перестройкой. Действительно, большая неравномерность вершины АЧХ придает разный вес спектральным откликам в пределах полосы фильтра, что требует трудной компенсации, а малая прямоугольность АЧХ приводит к перераспределению откликов на соседние полосы. Возникает императив: использование в фильтре ПЧ резонатора высокого порядка с высокой прямоугольностью. При этом множитель 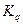уменьшается (при той же надежности разрешения). Если тракт последней ПЧ выполнен полностью цифровым, то есть и фильтрация в тракте осуществляется цифровым фильтром, то его прямоугольность может быть практически идеальной и множитель 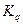близок к единице. В этом случае полоса разрешения практически равна шагу перестройки .

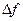Замечания:

1) До сих пор предполагалось, что шаг перестройки 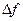равен полосе 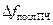фильтра последней ПЧ. Обычно СА сам подбирает 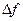в зависимости от установленной 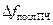. Если при текущей установке частотного диапазона анализа ( 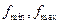) и числа шагов 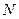получающееся отношение 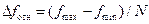больше 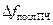, то СА устанавливает 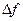= 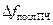, а компенсация производится при дисплейном детектировании с автоматически устанавливаемым эквивалентным видео-сглаживанием в 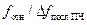раз. Если же получается 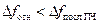, то опять СА устанавливает 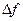= 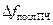, а реализуемое число частотных точек становится больше установленного в 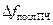/ 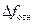раз.

2) При анализе разрешающей способности СА мы не учитывали влияние шумов и помех, в частности, фазовых шумов гетеродинов.

Классификация анализируемых сигналов

Классификация сигналов как упорядоченный перечень потенциальных для анализа объектов суть классификация подходящих функций времени во временной и частотной областях. Такая классификация не может быть замкнутой и должна ограничиваться субъективным отбором признаков, влияющих на конструктивные решения при разработке СА, на параметрические установки – при эксплуатации СА, на эффективность проводимого анализа, на интерпретацию результатов анализа.

На этапе разработки СА классификация сигналов двусторонне связана с широтой претензий на универсальность прибора: с одной стороны, перечень видов сигналов помогает уточнить параметрические и характеризационные границы желаемого, с другой – технические и стоимостные ограничения диктуют достижимые границы в пространстве сигналов.

Особая задача – интерпретация результатов измерения, в частности, математическая аппроксимация наблюдаемых результатов, например, амплитудных спектров; эта задача решается тем успешнее, чем четче априорное разделение сигналов на классы.

Нужно иметь в виду, что универсальный СА СВЧ должен удовлетворять потребностям анализа информативных сигналов не только в области радиоэлектроники, но в любых областях науки и техники, где используются СВЧ-сигналы для получения и передачи информации. Анализируемые сигналы могут поступать на СА как непосредственно с генератора, так и с выхода приемной антенны, с датчика экспериментальной аппаратуры, с выхода макета конструируемой аппаратуры и т.д.

1) Анализируемые колебания могут представлять детерминированный процесс, случайный процесс, квазидетерминированный процесс, смешанный детерминированно-случайный процесс.

а)Детерминированный процесс – математическая идеализация, поскольку любой сигнал всегда содержит долю случайных составляющих и не вполне прогнозируем на будущее. Например, сигнал любого генератора подвержен фазовым и амплитудным флуктуациям; любая цепь, через которую проходит сигнал, вносит стохастические элементы и шумы и т.д. Но выделение в определенных случаях и на приемлемых условиях и приближениях класса детерминированных сигналов совершенно необходимо для решения задач, где предполагается (хотя и приближенно) полное описание и полная прогнозируемость сигналов; именно эти задачи составляют большую часть радиотехники. Следует особо подчеркнуть, что один и тот же процесс, в зависимости от необходимой точности описания и прогнозирования и других требований, может быть отнесен или не отнесен к классу детерминированных процессов.

б)Случайные процессы – традиционная область путаницы, неточных представлений, нестрогих определений и других феноменов обыденного сознания в инженерной среде. Например, часто под случайными сигналами подразумевают неожиданные, спорадические, или редкие, или даже непериодические и т.д. сигналы. Иногда полагают, что для случайных процессов характерно отсутствие четкого описания, строгих характеристик, какой-либо возможности прогноза, экстраполяции. Степень неадекватности представлений о случайных процессах зависит от «просвещенности» того или иного работника.

в)Важность этого класса процессов для аппаратного анализа сигналов возрастает год от года и определяется колоссальным количеством видов флуктуаций и помех, сопровождающих генерацию и формирование сигналов, распространение их по каналам различной физической природы (линии передачи, атмосфера и т.д.), их прием, обработку, индикацию. С другой стороны, технологическое, системное, информационное развитие радиоэлектроники приводит к необходимости рассмотрения и учета все более слабых флуктуаций. Так, до определенного периода фазовые флуктуации высокодобротных генераторов СВЧ были просто интересным явлением, мало влияющим на эффективность радиотехнических систем, сейчас же качественные показатели ряда этих систем критически зависят от уровня фазовых флуктуаций применяемых генераторов. Надо признать, что радиоэлектроника и ее приложения являются «чемпионом» по использованию статистических подходов и методов. Ни в какой области технического знания так широко и глубоко не представлены статистические методы анализа, синтеза и оптимизации сигналов и систем, как в радиоэлектронике и ее разделах: беспроводной связи, радиолокации, оптическом и радио- зондировании сред (активном и пассивном), радионавигации и многих других.

г)Случайный процесс может быть описан на одном из двух уровней: на уровне распределений до некоторого порядка и некоторой точечности, или на уровне конечного числа числовых характеристик, в частности, уровне моментов. Уровень распределений более информативен, но более сложен в математической реализации и интерпретации результатов математического анализа и экспериментов. С одной стороны, теоретический вывод распределений вероятностей процесса (особенно второго и более высоких порядков) часто бывает неоправданно сложным или даже недоступным в конкретных физических и иных задачах; к тому же он может потребовать ряда допущений, которые затруднительно обосновать. С другой стороны, экспериментальное определение распределений случайных процессов предъявляет серьезные требования к измерительным приборам и системам обработки данных. Более того, существует огромное число теоретических задач, которые практически неразрешимы на уровне уже двумерных, а иногда даже одномерных распределений, по крайней мере, в аналитическом виде, пока не будут сделаны некоторые радикальные предположения, например, о гауссовости случайного процесса или поля. Достаточно привести примеры задач, которыми изобилует статистическая радиотехника: о линейном инерционном преобразовании, нелинейном безынерционном, тем более – нелинейном инерционном преобразовании случайного процесса. Зачастую такие радикальные предположения делаются в интересах «решения» задачи даже тогда, когда они заведомо не согласуются с реальностью задачи, а иногда даже со здравым смыслом. Насколько радикально, например, предположение о гауссовости процесса на входе нелинейного преобразования, в ситуации, когда оно неверно, видно уже из того, что для стационарного гауссовского процесса вся информация, содержащаяся в многомерном распределении любого порядка и любой точечности, содержится уже в корреляционной функции процесса, другими словами, описание на уровне распределений автоматически воспроизводится по корреляционной функции, т. е. по описанию на уровне первых и вторых моментов. Иногда в описании на уровне распределений нет особой необходимости и можно ограничиться описанием на уровне моментов. При использовании конечного числа моментов это описание заведомо неполное (если класс распределений не задан), но может удовлетворить потребности конкретного приложения. В других случаях переход на этот уровень может быть вынужденной мерой. Кроме того, иногда именно временная зависимость некоторых конкретных моментов представляет главный интерес. Описания на уровне моментов отличаются друг от друга наивысшим порядком участвующих в описании моментов. Среди этих описаний исключительное практическое значение имеет то, которое использует моменты до второго порядка включительно. Оно включает одноточечный момент первого порядка (математическое ожидание) и двухточечный момент второго порядка (корреляционную функцию), и может быть названо корреляционным описанием (рассмотрения на этом уровне описания часто называют «корреляционными теориями»). Используя СА, мы имеем дело, в первую очередь, именно с корреляционным описанием, доставляемое измерением спектральной плотности мощности (энергетического спектра) (кроме того, опционально, можно по получаемым данным рассчитывать моменты более высокого порядка, гистограммы распределений, сглаживать их и т.д.). Если есть основания считать случайный процесс стационарным по крайней мере в широком смысле (см. ниже и главу 6), то обратное преобразование Фурье от энергетического спектра есть ковариационная функция – второй двухточечный центральный момент как функция разности аргументов процесса. Важность и даже уникальность ковариационной функции как характеристики случайного процесса обусловлена двумя обстоятельствами. Во-первых, она полностью описывает структуру линейной статистической зависимости (корреляции) процесса. Во-вторых, ее Фурье-образ есть энергетический спектр процесса, то есть полностью описывает распределение средней мощности процесса по частотам. Вместе пара ЭС – КФ описывает статистическую динамику случайного процесса как во временной области (КФ), так и в частотной области (ЭС). В подборе математических аппроксимаций пар ЭС-КФ может помочь работа [2.5], где собран большой набор пар. Таким образом, еще один классификационный признак для случайных процессов – форма энергетического спектра (ковариационной функции).

д) Существует обширный и практически важный для радиоэлектроники класс случайных процессов, занимающих промежуточное положение между чисто-случайными и детерминированными процессами и называемых квазидетерминированными процессами. Временные реализации этих процессов детерминированы, но имеют случайные параметры. Например, это может быть синусоида со случайной амплитудой, или со случайными амплитудой и частотой; или это «пила» со случайным наклоном и/или периодом и/или эпохой; или это последовательность импульсов с одинаковой случайной шириной и/или постоянной случайной скважностью и т.д. и т.п. Имеется в виду, что случайные параметры реализуются в начале временной реализации процесса, а затем остаются постоянными. О квазидетерминированном процессе можно правильно судить, наблюдая не менее двух его реализаций: наблюдая только одну реализацию, можно решить, что это детерминированный процесс, но вторая реализация покажет, что это не так. Для того же, чтобы получить представление о свойствах случайных параметров (например, дисперсиях или распределениях), нужно наблюдать достаточно много реализаций.

е) Также промежуточное положение, но в другом смысле, занимают смешанные детерминированно-случайные процессы. Реализация такого процесса суть некоторая комбинация реализаций детерминированного и случайного процессов. К таким процессам относятся, в частности, детерминированные узкополосные сигналы, модулированные по амплитуде и/или по фазе (частоте) случайным процессом, и, наоборот, случайные процессы, модулированные по амплитуде и/или фазе детерминированным процессом. К этому классу примыкают формально детерминированные сигналы со сложными М-арными модуляциями (последние в некоторых случаях можно считать шумоподобными).

2) Сигнал может быть периодическим или апериодическим.

а) Детерминированный периодический процесс – функция времени, удовлетворяющая условию 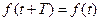для любого 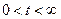, где 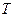называется периодом. Поскольку целое число величин 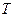– также период, иногда периодом называется наименьшая из величин, для которых удовлетворяется вышенаписанное условие. На практике периодическим часто считается сигнал, существующий на конечном интервале времени, если этот интервал много больше «периода». Как известно, преобразование Фурье от строго периодического процесса есть ряд Фурье, дающий амплитудный спектр в виде эквидистантной последовательности дельта-функций. Однако на практике спектральные линии имеют конечную ширину из-за конечности длительности анализируемой реализации и из-за неизбежных флуктуаций, делающих процесс приближенно периодическим, например, из-за фазовых шумов.

б) Случайный процесс общего вида не может быть периодическим в строгом смысле слова. Однако некоторые подклассы случайных процессов могут быть периодическими в условном смысле. Для квазидетерминированных процессов условная периодичность означает периодичность его реализаций (может быть, с разными периодами). Для детерминированно-случайных процессов вида «случайный процесс с детерминированной амплитудной модуляцией» условная периодичность означает периодичность модулирующей функции.

3)Случайный процесс может быть стационарным в каком-либо смысле, или нестационарным. Стационарность случайного процесса это свойство инвариантности тех или иных его характеристик относительно сдвига во времени. Поскольку число характеристик процесса бесконечно, то и видов стационарности бесконечное число. Для спектрального анализа случайных процессов особое значение имеют стационарность в широком смысле и стационарность в узком смысле (строгая стационарность). Часто при обсуждении вопросов аппаратного спектрального анализа изначально предполагают, что анализируемый процесс стационарен по крайней мере в широком смысле. На самом деле, спектроанализаторы рассматриваемого нами типа имеют определенные возможности спектрального анализа и некоторых типов нестационарных процессов. Оставляя пока рассмотрение этого вопроса, заметим только, что важный для приложений класс нестационарных процессов – периодически нестационарные случайные процессы, характеристики которых – периодичные функции времени.

4)По спектральному составу сигналы можно разделить на узкополосные, широкополосные и общего вида.

а) Сигнал называется узкополосным, если почти вся его мощность сконцентрирована в полосе 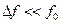вокруг характерной частоты (например, частоты максимальной спектральной амплитуды) 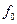. Например, узкополосным является сигнал генератора с нагруженной добротностью 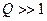. Многие современные радиотехнические цепи и системы предъявляют к сигналам требования по спектральной концентрации, для которых данное определение слишком неконкретно. Например, может требоваться, чтобы 99,9% мощности сигнала концентрировалась в полосе 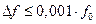. В диапазоне СВЧ класс узкополосных сигналов – основной; именно на такие сигналы рассчитаны линии передачи и многие другие устройства.

б) Широкополосным обычно называют сигнал, в спектре которого отношение максимальной и минимальной частот много больше единицы.

5)В математике функцию, отличную от нуля на конечном носителе, называют финитной. С этой точки зрения все сигналы – финитные функции времени, так как существуют лишь на конечном интервале времени. Более актуально сравнивать время существования сигнала с каким-либо интервалом, характерным для анализирующего прибора, например, временем развертки частоты, или временем сеанса измерения и т.п. Если сигнал финитен в такого рода смысле, его спектральные свойства имеют особые черты. Аналогично, если сигнал имеет финитный спектр, то он дает специфичные проявления во временной области. Это частные случаи общего принципа: ограничения на аргументы в частотной области порождают специфичное поведение во временной области, и наоборот. Например, квазимонохроматический детерминированный сигнал – частный вид узкополосных сигналов – допускает специфичные представления (через огибающую и фазу, через квадратуры) во временной области. Аналогично, узкополосный случайный процесс допускает похожие специфичные представления своей ковариационной функции.

6)Специфические классы сигналов составляют детерминированные и случайные процессы со скважностью во временной области или в частотной области. Сигналы со скважностью во временной области являются обобщением импульсной сигнальной последовательности, сигналы со скважностью в частотной области – обобщением периодических сигналов. В соответствии с высказанным принципом, первая группа сигналов имеет специфические характеристики в частотной области, вторая – во временной области.

Структура спектроанализатора

Современные спектроанализаторы (СА) в разной и все возрастающей степени используют цифровую обработку сигналов. Но описание структуры СА удобно и полезно начать с классической полностью аналоговой схемы.

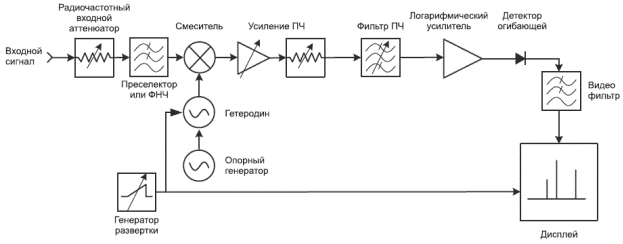
Структурная схема аналогового СА