Взвешенный мгновенный спектр

Вернемся к определению мгновенного спектра. Данное выше определение было названо частной конструкцией. Более общее определение мгновенного спектра [2.2, 2.3] связано с конструкцией, в которой в интеграл Фурье вводится скользящая (связанная с текущим временем) весовая функция:

;

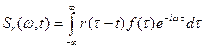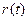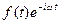получилась свертка функций и . Такая конструкция имеет два достоинства: она удобна как в аналитических преобразованиях, так и в учете искажающего спектральный анализ действия реальных цепей. Назовем такую конструкцию взвешенным мгновенным спектром.

То что 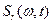– более общая конструкция мгновенного спектра, чем 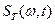, видно из того, что последняя есть частный случай первой при 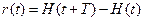, где

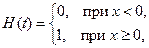
– функция Хевисайда (единичный скачок).

Важный частный пример весовой функции [2.3]:

.

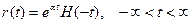Эта функция учитывает прошлое процесса с весом, экспоненциально убывающим по мере удаления от момента наблюдения. Заметим, что 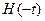– обращенный единичный скачок:

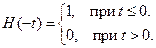
Такая весовая функция отражает влияние на спектральный анализ реальных цепей с однорелаксационным затуханием, например, резонансных фильтров первого порядка; параметр 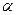учитывает скорость затухания.

Плотности мощности

Было бы привлекательно построить такую спектральную характеристику, которая служила бы временной плотностью некой интегральной характеристики, от которой она получалась бы дифференцированием по времени. Осуществлению этой идеи мешает комплексный характер «истинного» спектра и текущего спектра. Наиболее просто и удобно реализовать эту идею, взяв за основу не текущий спектр, и не амплитудный текущий спектр, а спектр мощности сигнала. Как показано в главе 6, спектральной характеристикой случайного процесса является спектральная плотность мощности (энергетический спектр), по определению являющийся средней мощностью на единицу полосы процесса. Аппаратную оценку этой характеристики дает величина, пропорциональная квадрату амплитудного спектра, полученного достаточно долгим усреднением по реализации процесса, то есть квадрату модуля текущего спектра. Замечательно, что эта оценка сохраняет свой смысл спектральной плотности мощности (но уже без добавления слова «средней») и для детерминированного сигнала. Удобно, что эта функция частоты не только действительна, но и всюду неотрицательна, а также связана простым интегральным соотношением с мощностью сигнала.

Итак, пусть по-прежнему 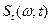– текущий (комплексный) спектр сигнала, 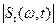– текущий амплитудный спектр сигнала, тогда 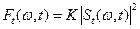– можно назвать текущим энергетическим спектром ( 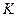– коэффициент с размерностью сек^-1). Смысл 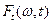раскрывается равенством:

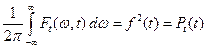
(в правой части – мгновенная мощность сигнала). Оно означает, что 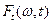это спектральная плотность мгновенной мощности – мощность на единицу (циклической) частоты.

Полезно и поучительно контролировать размерности рассматриваемых величин. Пусть сигнал и все связанные с ним величины приведены к сопротивлению в 1 Ом, в такой системе мощность равна квадрату напряжения. Тогда размерности: 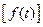=В; 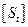=В/Гц; 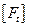=В²/Гц=Вт/Гц.

Следуя Пейджу [2.4], введем такую всюду неотрицательную функцию частоты 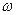и времени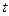 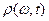(с размерностью Вт), что

.

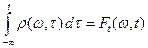Дифференцируя это равенство по 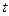, получаем:

,

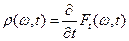а интегрируя его по 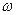, имеем

,

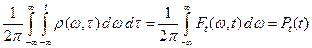откуда следует, что 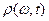суть спектрально-временная плотность мощности сигнала.

Можно пойти дальше в образовании плотностей мощности. Пусть сигнал снимается с апертуры 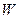. Тогда можно ввести такую всюду неотрицательную функцию частоты 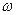, точки на апертуре 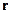и времени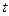 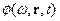, что

.

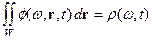Эту функцию с размерностью 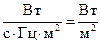назовем спектрально-пространственно-временной плотностью мощности сигнала.

Полезны также пространственно-временная плотность мощности :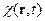

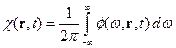
с размерностью 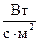и спектрально-пространственная плотность мощности :

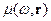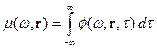
с размерностью .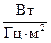

Какой спектр измеряет конкретный спектроанализатор?

Теперь, после рассмотрения различных спектральных характеристик, возникает вопрос: какую из них измеряет спектроанализатор? Конечно, точный и подробный ответ на этот вопрос возможен только после определения структуры СА, но принципиальную часть ответа возможно сформулировать уже сейчас.

Забегая вперед, будем иметь в виду СА последовательного типа (см. 2.1.2), с переносом спектра с помощью супергетеродинирования, гетеродин которого (первый, если их больше одного) суть синтезатор частоты (СЧ), последовательно генерирующий сетку частот с устанавливаемыми оператором или по умолчанию диапазоном и шагом перестройки.

Обозначим:

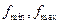– минимальная и максимальная частоты перестройки СЧ;

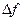– шаг перестройки СЧ;

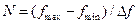– число частотных подынтервалов;

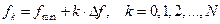– частотные точки;

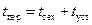– время перестройки СЧ на следующую частотную точку;

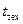– технической время перестройки СЧ;

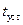– длительность переходных процессов при перестройке СЧ (время установления);

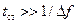– время «стояния» СЧ на частотной точке;

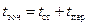– время, затрачиваемое на одну частотную точку;

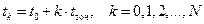– момент времени, соответствующий частотной точке ;

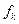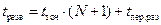– время, затрачиваемое на одну развертку частоты;

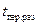– время переключения на следующую развертку частоты.

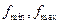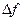СА с установленными предварительно параметрами и последовательно «становится» на частотные точки 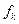, от первой 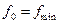до последней 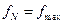; в каждой из них СА находит оценку усеченного мгновенного спектра

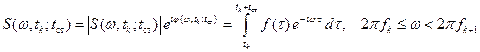
участка спектра шириной 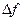. Если это скалярный СА, то он выдает в качестве результата лишь оценку амплитудного спектра:

,

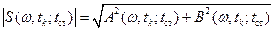где

.

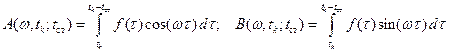Если же это векторный СА, то он выдает в качестве результата оценку комплексного спектра, скорее всего, в виде двух характеристик: амплитудного спектра 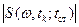и фазового спектра

.

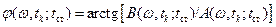Определим скважность спектрального анализа как отношение времени, затрачиваемого на одну развертку, к времени «стояния» на одной частотной точке:

.

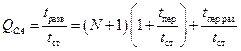Обычно 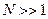и составляет несколько десятков или сотен, поэтому последним слагаемым справа можно пренебречь; если второе слагаемое в скобках много меньше единицы, то .

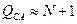Итак, СА последовательного анализа измеряет мгновенный усеченный амплитудный спектр (или амплитудный и фазовый спектры) по графику, в котором:

– участку спектра шириной 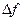соответствует время анализа ;

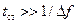– каждый участок спектра шириной 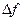анализируется на своем интервале времени;

– разные участки спектра разнесены по времени: минимально – на 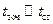, максимально – на ;

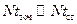– анализ каждого участка спектра повторяется установленное оператором или по умолчанию число раз со скважностью .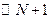

Искажающее действие реального фильтра

Спектральный прибор принципиально вносит свои искажения в оценку спектра сигнала. На этом этапе изложения нет смысла проводить глубокий анализ этих искажений; мы ограничимся простой демонстрацией присутствия искажений. Пусть на вход фильтра ПЧ с импульсной характеристикой 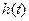поступает сигнал 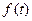на интервале 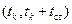. Сигнал на выходе фильтра равен

.

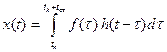Если 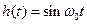(идеальный фильтр пропускания частоты 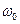), то

,

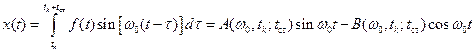и получается оценка истинного амплитудного спектра на частоте :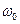

.

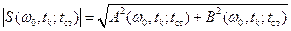Если же для реального полосового фильтра с потерями с центральной частотой 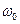принять

,

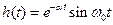то получается

,

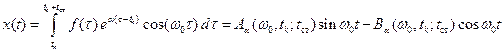где

.

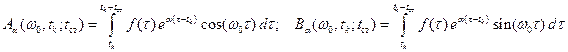Как видим, получается мгновенный спектр не функции 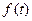, а взвешенной функции 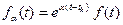. В более общем случае реального полосового фильтра с центральной частотой 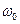[2.2] импульсная характеристика имеет вид:

,

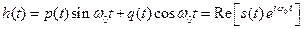где 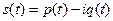, и на выходе фильтра:

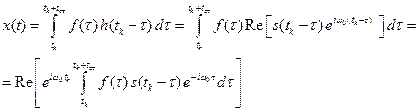
то есть получается мгновенный спектр взвешенной функции .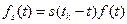

Разрешающая способность последовательного анализа

На протяжении веков применения спектрального анализа, сначала в оптике, а затем и в радиотехнике, центральным вопросом качества анализа был вопрос разрешающей способности анализа. Выражаясь современным языком, можно сказать, что «… разрешающая способность – важнейшая метрологическая характеристика (спектрального) анализатора» [2.2]. На этом этапе изложения мы лишь наметим общие контуры проблемы. Классический подход к этому вопросу состоит в следующем. В самом общем смысле под разрешающей способностью спектроанализатора понимается его способность разрешить (то есть «видеть» по отдельности) две соседние спектральные линии в сигнале. В общем случае эти линии могут представлять собой локальные максимумы спектра с достаточно глубокими провалами вокруг этих максимумов, то есть иметь разные спектральные амплитуды и разные спектральные ширины. Мы сразу сузим задачу, предположив, что линии имеют бесконечно малую ширину и одинаковые амплитуды. Первое предположение на практике означает, что линии много уже полос фильтров анализатора, оба предположения – что мы хотим оценить предельное разрешение.

Количественной мерой разрешающей способности является наименьший частотный интервал (интервал разрешения) между двумя спектральными линиями, при котором они еще разрешаются спектроанализатором. Чем меньше интервал разрешения, тем лучше разрешающая способность. Но что значит «разрешаются» в точном математическом смысле? Об этом условимся чуть ниже.

Будем, как прежде, иметь в виду последовательный спектральный анализ. Сначала рассмотрим гипотетический СА с плавной перестройкой спектра, в котором дискретизации по частоте нет: спектр входного сигнала плавно (и очень медленно, чтобы результат анализа прямо не зависел от скорости перестройки) сдвигается путем непрерывного изменения частоты гетеродина. Для рассмотрения данной задачи удобно считать, что сдвигается не спектр, а анализирующий фильтр плавно перестраивается, не меняя ни формы АЧХ, ни ее ширины.

Сначала предположим, что в спектре входного сигнала имеется одна спектральная линия с частотой 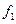. По мере перестройки фильтра амплитуда выходного сигнала фильтра описывает кривую в функции времени, совпадающую с АЧХ как функцией частоты. При совпадении резонансной частоты фильтра с 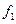кривая достигает максимума.

Пусть теперь в спектре входного сигнала имеются две спектральные лини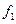и и 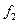одинаковой интенсивности. В резонаторе фильтра теперь одновременно существуют колебания двух частот и происходят биения с частотой 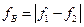. Амплитуда сложного выходного колебания теперь не постоянна, а периодична с периодом 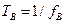, повторяя с этим периодом свое наибольшее значение, равное сумме выходных амплитуд обеих спектральных составляющих. Поскольку перестройка резонатора происходит очень медленно, можно регистрировать эту сумму как амплитуду выходного сигнала. Каждая из выходных амплитуд отдельных линий повторяет одногорбую кривую, рассмотренную выше, максимумы кривых отстоят друг от друга на 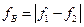. При достаточно большом 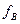суммарная кривая имеет провал (локальный минимум) на средней частоте 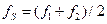и «горбы» (локальные максимумы) на частотах 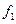и 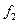. Если теперь сближать частоты 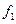и 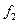, то выраженность провала уменьшается, затем исчезает вовсе, затем в точке 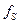образуется максимум, а локальные максимумы в точках 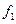и 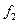исчезают.

Теперь мы готовы дать математическое определение термину «разрешается». Это можно сделать по-разному. Наиболее простое и удобное определение таково: линии разрешаются, если частотное расстояние между ними больше или равно частотному интервалу разрешения, который, в свою очередь, равен такой 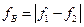, при которой отношение амплитуды 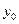в провале к амплитуде 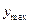максимумов равно заданному числу:

.

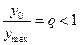Это уравнение можно, в принципе, решить относительно 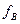, если задать АЧХ конкретного фильтра. Например, для простого резонансного контура с добротностью 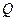, относительная АЧХ которого:

,

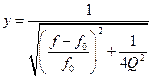решение уравнения имеет вид [2.2]:

.

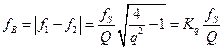Как видим, полоса разрешения для простого резонансного контура равна произведению двух множителей. Множитель 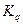определяется только произвольно принятым нами значением 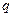, составляет порядок нескольких единиц, например, при 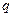=1/3, 1/2,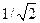 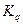=5.92, 3.87, 2.65 соответственно, и отражает надежность разрешения: чем глубже критический провал, тем больше 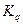. Множитель 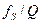есть ничто иное, как полоса того же фильтра при его настройке на 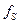. При использовании фильтра более высокого порядка, имеющего более высокий коэффициент прямоугольности, множитель 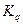уменьшается (при той же надежности разрешения).

Рассмотренная нами разрешающая способность называется статической, поскольку не учитывает временные эффекты, подобные влиянию момента начала сигнала, конечной скорости перестройки и т.п. Учет этих факторов довольно сложен и приводит к понятию динамической разрешающей способности, которую мы пока не рассматриваем.

Вспомним теперь, что в современном СА в качестве гетеродина используется синтезатор частот, благодаря чему спектр сигнала сдвигается на дискретные значения, кратные величине 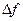. Опять, как и при рассмотрении последовательного анализа, удобно считать, что сдвигается не спектр, а анализирующий фильтр (на этот раз не плавно, а шагами по 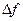) перестраивается, не меняя ни формы АЧХ, ни ее ширины. Резонатор анализирующего фильтра последовательно настраивается в резонанс на частотную точку 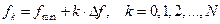к моменту времени 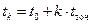и остается в этой настройке в течение времени 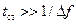, затем к следующему моменту времени перестраивается на следующую частотную точку.

Заметим, что если бы фильтр на самом деле перестраивался, то для сохранения его полосы 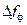пришлось бы по мере перестройки менять его добротность в соответствии с формулой 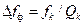, но поскольку на самом деле анализирующий фильтр есть постоянный во времени фильтр ПЧ, постоянство его полосы выполняется автоматически. Далее, заметим, что полоса анализирующего фильтра (фильтра ПЧ) должна быть не больше и не меньше, а равна шагу частотной перестройки: 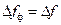. Действительно, если будет 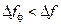, то часть информации об анализируемом спектре сигнала будет утеряно; если будет 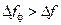, то возникнет неоднозначность отсчетов.

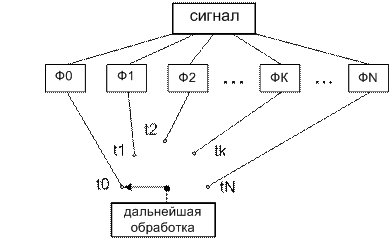
Теперь мы готовы представить удобную виртуальную модель обработки сигнала в вышеописанных условиях, полезную не только при анализе разрешающей способности СА. Модель иллюстрируется рис. 2.1.1 и представляет схему параллельного спектрального анализа с последовательным опросом каналов (фильтров).