Усеченный мгновенный спектр
Главным недостатком спектральной характеризации сигнала с помощью преобразования Фурье является отсутствие локализации по времени; предоставляемая при этом, в соответствии с соотношением неопределенности «время-частота», бесконечная локализация по частоте не используется по техническим причинам. Отсутствие локализации по времени не позволяет контролировать какие-либо временные изменения спектральной характеристики. Требуются такие спектральные характеристики, которые бы совмещали умеренные локализации по времени и по частоте, тем самым давая промежуточное представление сигнала между временной и частотной областями. Радикальное решение этой задачи – представление сигнала в вейвлетном базисе. Однако и в Фурье-базисе имеются некоторые возможности. Один из вариантов – введение спектральной характеристики, называемой мгновенным спектром.
Частная конструкция мгновенного спектра – функция частоты и времени, определяемая как [2.2]:
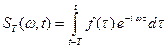 ,
,
то есть это спектр отрезка сигнала длительностью 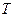 , непосредственно предшествующего моменту наблюдения
, непосредственно предшествующего моменту наблюдения 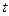 . Назовем эту конструкцию усеченным мгновенным спектром. По мере течения времени мгновенный спектр получается скользящим интегрированием по перемещающемуся отрезку постоянной длины.
. Назовем эту конструкцию усеченным мгновенным спектром. По мере течения времени мгновенный спектр получается скользящим интегрированием по перемещающемуся отрезку постоянной длины.
Чтобы лучше понять смысл новой характеристики, выразим ее через текущий спектр:
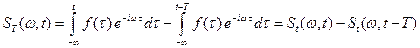 ,
,
то есть на каждой частоте 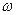 мгновенный спектр равен приращению текущего спектра на интервале времени длиной
мгновенный спектр равен приращению текущего спектра на интервале времени длиной 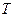 , предшествующем моменту наблюдения
, предшествующем моменту наблюдения 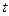 . Предполагая, что функция текущего спектра
. Предполагая, что функция текущего спектра 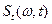 дифференцируема по аргументу
дифференцируема по аргументу 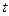 , при малых
, при малых 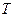 можно это приращение выразить так:
можно это приращение выразить так:
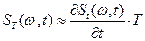 .
.
Эту же приближенную формулу можно было получить сразу дифференцированием интеграла по параметру 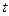 в определении мгновенного спектра.
в определении мгновенного спектра.
Кроме пояснения смысла мгновенного спектра, формула дает полезный рецепт для приближенной оценки верхней грани скорости изменения текущего спектра нестационарного сигнала на каждой частоте 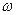 . Действительно, с одной стороны, из этого равенства следует:
. Действительно, с одной стороны, из этого равенства следует:
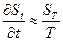 ;
;
с другой стороны, записав комплексный текущий спектр в виде
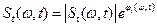
и дифференцируя по 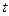 , получаем:
, получаем:
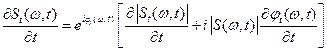 .
.
Приравнивая правые части равенств и переходя к модулям, имеем:
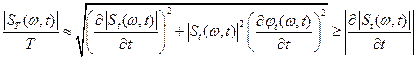 ,
,
и мы получили искомое неравенство:
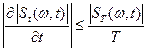 .
.
Дата добавления: 2016-02-20; просмотров: 910;
