Другие характеристики физического спектра радиоимпульсного процесса
Огибающая физического спектра, также как и у математического описывается функцией вида sinx/x. Гармоника спектра в максимуме огибающей может и не образоваться. Это может быть в спектре радиоимпульсных последовательностей второго и четвертого видов, структура которых позволяет устанавливать положение огибающей спектра и положение гармоник спектра на оси частот совершенно независимо.
Поясним это. При настройке контура на частоту wр (w0=wр)свободные колебания, оставшиеся в контуре после прекращения радиоимпульса, будут иметь максимальную амплитуду. Однако разность фаз между колебаниями, оставшимися в контуре после соседних радиоимпульсов, может отличаться и, возможно, существенно, от 2p. В результате синфазного сложения колебаний не произойдет и гармоника спектра на этой частоте не сформируется. А на тех частотах, где создадутся условия для их синфазного сложения, амплитуды этих колебаний могут оказаться небольшими. В результате возникнет накопительный резонанс, хотя получившаяся гармоника спектра и не будет иметь максимальную амплитуду.
Теперь рассмотрим положение нулей огибающей физического спектра. Когда частоты радиоимпульса wр и колебательного контура wо различны, в последнем возникают биения, амплитуда которых изменяется с частотой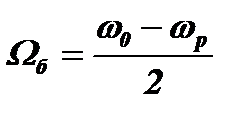 
. Если за время импульса t биения в контуре совершат один или несколько целых полупериодов 
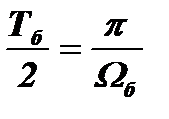, то после окончания радиоимпульса свободные колебаний в контуре не возникнут. В результате гармоника спектра не сформируется, даже если будут выполнены условия для синфазного сложения свободных колебаний.
В этом случае:
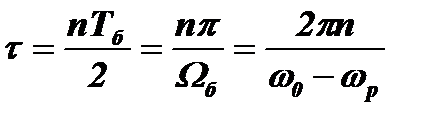, где n=0; ±1; ±2; ±3;...
Отсюда следует, что нули спектра образуются на частотах:
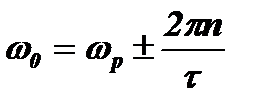или 
.
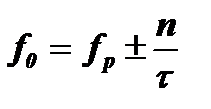Эти значения wо совпадают с частотами нулей математического спектра радиоимпульсной последовательности.
Нетрудно заметить, что спектры последовательностей видеоимпульсов и радиоимпульсов при одинаковой частоте повторения имеют одинаковое расположение нулей огибающей относительно ее максимума. Однако физические причины образования этих нулей оказываются совершенно различными. В первом случае нули образуются за счет взаимной компенсации колебаний одной и той же частоты, возбуждаемых передним и задним фронтами видеоимпульса. Во втором случае причиной образования нулей является взаимная компенсация колебаний двух разных частот в конце каждого полупериода биений.
Рассмотрим фазовый спектр радиоимпульсной последовательности. В этом спектре, также, как и в фазовом спектре последовательности видеоимпульсов, фазы гармоник изменяются на p после перехода частоты контура wо через каждый последующий ноль огибающей амплитудного спектра. Этот переворот фазы гармоник спектра вызван особенностью биений – изменением фазы их колебаний на 180о при переходе амплитуды биений через ноль в каждом полупериоде.
В результате фаза биений, возникающих в контуре, формирует фазовую структуру спектра процесса, аналогичную фазовой структуре спектра, полученного при математическом анализе.
Обратим внимание на интересное обстоятельство, связанное с поворотом фазы гармоник в спектре видеоимпульсной последовательности и в спектре радиоимпульсной последовательности. В обоих спектрах фаза гармоник при переходе через нуль переворачивается на 180о, хотя причины этого переворота фазы, также как и причины образования нулей спектра различны. В первом случае нуль спектра образуется благодаря взаимной компенсации двух колебаний одной и той же частоты wо (сложение колебаний, образованных передним и задним фронтами одного и того же импульса). Во втором случае происходит взаимная компенсация колебаний разных частот wо и wр, которые образуют биения.
Мы рассмотрели в этом разделе образование физического спектра радиоимпульсной последовательности и убедились в его тесной связи с ее математическим спектром. В заключение раздела рассмотрим один из парадоксов спектральной теории, объяснение которого показывает важность правильного представления физической картины формирования спектра какого-либо сигнала.
Дата добавления: 2016-04-19; просмотров: 1215;