Условия передачи максимальной мощности от источника энергии к нагрузке.

Практически во всех энергетических и информационных системах происходит передача электрической энергии в той или иной ее форме от некоторого источника к некоторой нагрузке. Как правило, в нагрузку необходимо передать максимально возможную часть мощности источника. В большинстве случаев вообще желательно передать в нагрузку всю мощность, имеющуюся в источнике. Так, например, очевидно, что нет необходимости сохранять какую-либо часть мощности в электростанции. Лучше её всю передать потребителям электроэнергии. Нет необходимости оставлять сколько-нибудь мощности в передатчике радиостанции. Для увеличения дальности и повышения качества связи желательно направить всю его мощность в антенну. Образно говоря, мы хотели бы передать всю мощность из источника в нагрузку, также как мы переливаем жидкость из одного сосуда в другой.

Рис. 6.1 Сообщающиеся сосуды

Однако на практике так не получается. Силы, действующие в электрической системе, не позволяют это сделать. И если сравнивать передачу мощности от источника в нагрузку с переливанием жидкости из сосуда в сосуд, то можно представить источник и нагрузку в виде двух одинаковых сосудов, сообщающихся через перемычку с краном (рис. 6.1). Нальём в сосуд-источник жидкость при закрытом кране, а потом откроем его. Мы увидим, что уровни жидкости сравнялись, и в сосуд-нагрузку попала только половина жидкости (мощности), а другая половина осталась в сосуде-источнике. Чтобы перелить её в сосуд-нагрузку до конца, надо приложить к оставшейся жидкости дополнительные силы, например, поднять сосуд-источник над уровнем жидкости в сосуде-нагрузке или выдавить жидкость из сосуда-источника каким-нибудь поршнем. То же самое происходит и при передаче электрической энергии. Таким образом, при построении систем, так или иначе связанных с такой передачей, возникает важная задача - как обеспечить эту передачу и, в частности, как выбрать нагрузку, чтобы в неё попала максимальная мощность источника.

Рассмотрим простую электрическую схему, изображённую на рис. 6.2. Это цепь постоянного тока. Общее сопротивление цепи равно R=R_И+R_Н. Ток в цепи: I=U/R. Мощность, выделяемая в нагрузке, будет равна:

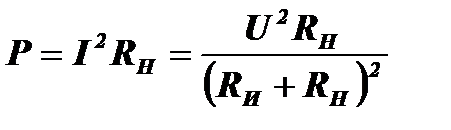Чтобы найти максимум этой мощности, необходимо найти производную 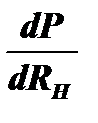по правилу дифференцирования дроби: 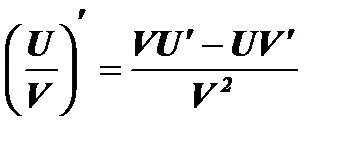и приравнять её числитель нулю.

Тогда: U²(R_И+ R_Н)²-2U²R_Н (R_И+ R_Н)=0.

Отсюда: 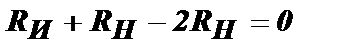или R_И = R_Н

При соблюдении этого условия в нагрузку отдаётся мощность

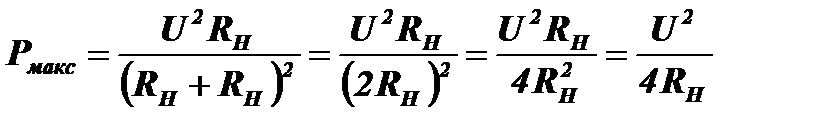. Нетрудно видеть, что на внутреннем сопротивлении источника выделяется такая же мощность: .

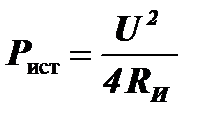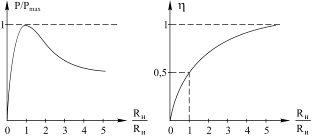
а) б) Рис. 6.3 Зависимость мощности, выделяемой в нагрузке (а) и КПД системы (б) от отношения сопротивления нагрузки к внутреннему сопротивлению источника

КПД системы передачи мощности от источника в нагрузку при этом составляет 0,5, поскольку половина мощности выделяется на сопротивлении источника. Таким образом, в наилучшем случае только половина мощности попадёт из источника в нагрузку. Во всех иных случаях доля этой мощности будет ещё меньше. На рисунке 6.3 показана зависимость относительной мощности, передаваемой в нагрузку P/P_max и КПД системы η от соотношения R_Н/R_И.

Теперь рассмотрим источник переменного тока, который развивает на произвольной частоте ω напряжение u=Ucosωt и в общем случае имеет комплексное внутреннее сопротивление Z_И=R_И+X_И, где R_И и X_И соответственно активная и реактивная части его внутреннего сопротивления. Сопротивление нагрузки также состоит из активной и реактивной частей Z_Н=R_Н+X_Н (рис.6.4).

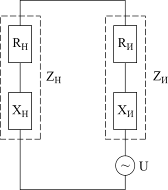
Рис. 6.4 Схема цепи переменного тока

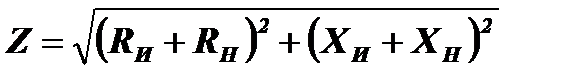Общая активная нагрузка, на которую работает источник, будет равна (R_И+R_Н), а общая реактивная часть этой нагрузки будет равна (X_И+X_Н). Полное сопротивление этой смешанной активно-реактивной цепи определяется по формуле: . Ток в этой цепи равен 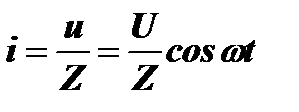. Тогда активная мощность, выделяемая в нагрузке, будет равна:

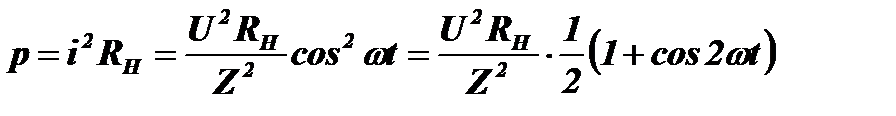
Средняя мощность за период:

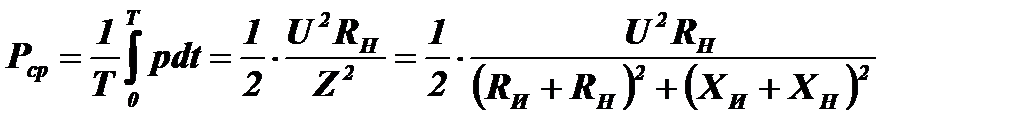
Сначала определим роль реактивных сопротивлений в получении максимума этой мощности. Очевидно, что при любых значениях R_И и R_Н активная мощность достигнет наибольшей величины при условии (X_И+X_Н)=0, т.е. при взаимной компенсации реактивных сопротивлений источника и нагрузки X_И=−X_Н.

Аналогичная картина возникает в обычном колебательном контуре при резонансе. Когда реактивное сопротивление емкости контура становится равным, но противоположным по знаку реактивному сопротивлению индуктивности, в последовательном контуре создаются условия для получения максимального тока.

При X_И=−X_Н средняя мощность за период будет равна: 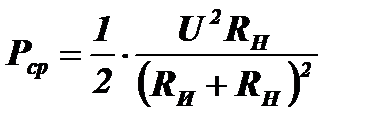. Взяв производную этой величины по R_Н и приравняв ее нулю, мы снова получим условие для выделения максимальной мощности в нагрузке в виде равенства R_И=R_Н.

Таким образом, для получения максимальной мощности в нагрузке, активные сопротивления источника и нагрузки должны быть равны, а их реактивные сопротивления должны быть равны по абсолютной величине, но иметь противоположные знаки. Для взаимной компенсации напряжения на реактивных сопротивлениях источника и нагрузки должны быть сдвинуты по фазе на 90⁰ в разные стороны относительно тока в цепи. Эти напряжения являются, как бы, зеркальным отображением друг друга.

Если представить сопротивления источника и нагрузки в виде комплексных чисел, то нетрудно заметить, что для передачи максимальной мощности от источника в нагрузку сопротивления источника энергии и потребителя энергии должны быть комплексно сопряжёнными Z_И=R_И+iX_И и Z_Н=R_Н−iX_Н.

Следует отметить, что согласование нагрузки и источника является очень широким понятием и проявляется в самых разных областях.

Например, именно по этой причине поединки боксеров проводятся в разных весовых категориях, где соперники имеют примерно равный вес. Ведь боксер тяжелого веса не сможет передать мощность своего удара легковесу, поскольку тот просто отлетит прочь. Точно также легковес не сможет передать мощность своего удара тяжеловесу, поскольку, ударив, сам отскочит назад. Передача мощности при ударе будет только тогда эффективной, когда источник удара и «нагрузка», по которой наносится удар, имеют одинаковый вес.

Возьмем более близкий нам пример: электрическая батарея нагревает электрическую плиту. Каким должно быть сопротивление плиты, чтобы она отбирала от батареи максимум мощности? Количество тепла, выделяемого электроплитой, пропорционально току в цепи. Если сделать сопротивление плиты значительно больше, чем сопротивление батареи, то ток в цепи будет мал и тепла в электроплите выделится очень мало. Если сопротивление плиты сделать значительно меньше, чем сопротивление батареи, то ток в цепи станет большим, но тепло будет выделяться, в основном, в электрической батарее, а не в плите. В обоих случаях электроплита дает мало тепла. Наибольшее количество тепла будет выделяться в электроплите, когда сопротивления плиты и батареи будут равны. В этом случае и в батарее и в плите будет выделяться одинаковое количество тепла, равное только 50% от общей мощности батареи.

Для согласования сопротивлений источника и нагрузки существует много способов. В механике для передачи максимума мощности используется рычаг. Расширяющийся раструб рупорной антенны согласовывает волновод со свободным пространством. Врач использует стетоскоп, чтобы согласовать акустические сопротивления своего уха и грудной клетки пациента. Сердце человека также согласовано по сопротивлению с системой артерий и вен, хотя это согласование с возрастом ухудшается.

<24 25 26 272829 30 >

Дата добавления: 2016-04-19; просмотров: 13032;