Расположение гармоник физического спектра последовательности прямоугольных радиоимпульсов
Возникновение резонанса в колебательном контуре, который возбуждается последовательностью радиоимпульсов, происходит иначе, чем при его возбуждении последовательностью видеоимпульсов.
Напомним, как развиваются в этом случае процессы в колебательном контуре с высокой добротностью при подаче на него радиоимпульса длительностью t. Если частота заполнения радиоимпульса wр и собственная частота колебаний контура wо не равны, то в контуре возникнут биения с периодом изменения амплитуды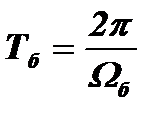 
( 
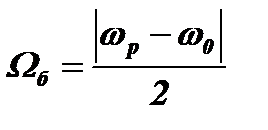) и с частотой заполнения 
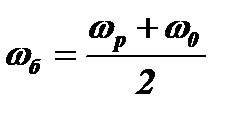.Биения будут существовать в контуре в течение времени t.При равенстве wр = wо возникает резонанс и амплитуда колебаний в контуре будет непрерывно расти в течение времени t. Во всех случаях после окончания импульса в контуре останется свободное колебание с частотой wо, длительность которого из-за высокой добротности контура будет значительно превышать длительность импульса t. Начальная амплитуда и начальная фаза этого свободного колебания будут определяться, соответственно, амплитудой и фазой биений в момент времени τ.
Для того чтобы возникла гармоника спектра, необходимо, чтобы разность фаз Dj между свободными колебаниями, остающимися в контуре после каждого импульса, равнялась 2pm, где m = 0;±1;±2;±3;..., то есть чтобы эти колебания складывались синфазно, амплитуда колебаний в контуре увеличивалась и возникал накопительный резонанс. Рассмотрим, от чего зависит эта разность фаз при воздействии на контур двух соседних радиоимпульсов. Действие остальных импульсов последовательности на контур будет аналогичным в силу принципа суперпозиции.
Вернемся к рис. 4.44, где вверху изображена пара радиоимпульсов, поступающих в контур, а ниже – колебания в контуре, возникшие под действием, соответственно, первого и второго импульсов. Определим разность фаз Dφ, которая образуется между этими двумя колебаниями в момент времени Т2, когда оба импульса закончились, третий еще не начался и в контуре существуют только свободные колебания, вызванные первыми двумя импульсами. Интересующая нас разность фаз будет определяться двумя факторами.
Первым из этих факторов является набег фазы колебаний, вызванных каждым из двух импульсов, от момента возникновения импульса до момента Т2. В периоды существования в контуре радиоимпульса (от 0 до τ1 для первого импульса и от Т1 до τ2 для второго импульса) в контуре образуются биения с частотой 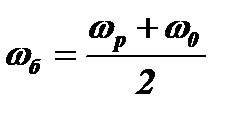. Набег фазы биений за время импульса τ будет равен 
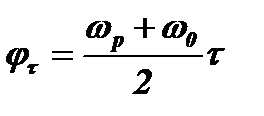. После окончания импульса (от τ1 до Т2 для первого колебания и от τ2 до Т2 для второго колебания) в контуре останутся только свободные колебания, имеющие частоту ωо. Набег фазы в эти периоды составит для первого и второго колебаний, соответственно, 
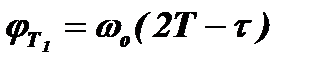и 
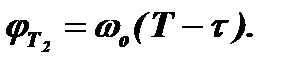Таким образом, полный набег фазы от момента возникновения импульса до момента Т2 для первого и второго колебаний равен, соответственно, 
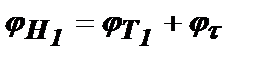и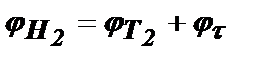 
.
Вторым фактором является начальная фаза колебаний. Для первого импульса это будет фаза, с которой он начнется в момент t=0 (обозначим эту фазу φ01), а для второго импульса – фаза, с которой он начнется в момент t=Т1 (обозначим эту фазу φ02).
С учетом обоих факторов полная фаза первого колебания в момент Т2 будет равна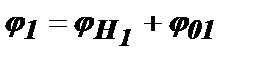 
, а полная фаза второго колебания в этот момент – 
.
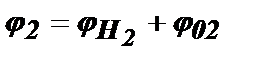Для синфазного сложения этих колебаний необходимо, чтобы разность фаз между ними Dφ была равна 2πm:
Dj =φ1–φ2=(jН1+j01) - (jН2+j02) = (jН1 -jН2) + (j01 - j02) = 2pm,
где m = 0; ±1; ±2; ±3;...
Рассмотрим сначала первое слагаемое этого выражения (jН1-jН2), не связанное с начальной фазой импульсов. Подставляя значения величин, входящих в jН1 и jН2, получим:
jН1 -jН2 = (jТ1 + jt) - (jТ2 + jt) = jТ1 + jt - jТ2 - jt = jТ1- jТ2= 2wоТ - wоТ=wоТ.
Эта разность фаз не зависит от длительности радиоимпульса и верна для любой радиоимпульсной последовательности.
Теперь рассмотрим второе слагаемое (j01-j02),зависящее от начальных фаз соседних радиоимпульсов.
У радиоимпульсных последовательностей первого и второго видов начальные фазы всех импульсов одинаковы. Поэтому разность (j01-j02) в этих случаях всегда будет равна нулю, а условие синфазного сложения колебаний и получения резонанса имеет вид: Dj =(jН1-jН2)=w0T=2pm.
Отсюда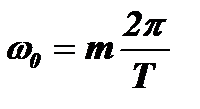 
. Учитывая, что 
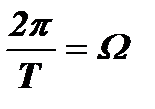, получим значения частот, на которых в колебательном контуре возникнут гармоники спектра: 
.
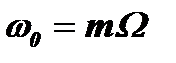Начальную фазу каждого импульса радиоимпульсной последовательности третьего вида определяет колебание с частотой wр. Разность между начальными фазами соседних n-го и n+1-го импульсов равна:
j01-j02=wрnT-wр(n+1)Т=-wрT.
Условие синфазного сложения колебаний и получения резонанса в этом случае имеет вид:
Dj =(jН1-jН2)+(j01-j02)=w0T-wрT=(w0-wр)T=2pm,
а значения частот колебательного контура, на которых возникнут гармоники спектра, будут равны:
w0 = wр ± mW.
Основная гармоника возникнет в контуре на частоте заполнения радиоимпульса wр, а остальные гармоники будут располагаться по обе стороны от нее на частотах, кратных частоте повторения импульсов W.
У радиоимпульсной последовательности четвертого вида начальная фаза радиоимпульсов формируется посторонним колебанием, имеющим частоту wП. Тогда:
j01 - j02=wПnT - wП(n+1)T = -wПT.
Условие формирования гармоники в этом случае:
Dj=w0T-wПT=(w0-wП)Т=2pm,
а гармоники спектра возникнут на частотах:
w0=wП±mW.
Также, как и в предыдущем случае, положение гармоник спектра не зависит от частоты заполнения радиоимпульсов, а огибающая спектра и гармоники «развязаны» друг относительно друга. Можно раздельно управлять положением огибающей на оси частот, меняя wр, и положением гармоник, меняя wП.
И, наконец, радиоимпульсная последовательность пятого вида не будет иметь постоянных гармоник спектра, поскольку случайное значение начальной фазы каждого радиоимпульса не позволяет сформироваться условиям синфазного сложения свободных колебаний, оставшихся в колебательном контуре после каждого импульса. Спектр сигнала «размывается» вдоль оси частот, становится сплошным.
Таким образом, положение гармоник физического спектра радиоимпульсной последовательности при ее наблюдении с помощью перестраиваемого по частоте анализатора спектра (колебательного контура) полностью совпадает с положением гармоник математического спектра, полученного с помощью теории спектров периодических и почти периодических функций.
Дата добавления: 2016-04-19; просмотров: 989;