Напряжение. Мощность. КПД. Вращающий момент
Пусть генератор постоянного тока вырабатывает ЭДС ℰ при циклической частоте тока w. Пусть внутреннее сопротивление генератора (активное сопротивление обмотки якоря) равно r, а сопротивление нагрузки – R. Выясним, каково напряжение U на зажимах генератора, каковы его полная N, полезная Р и «бесполезная» Q мощность, чему равен КПД и вращающий момент М на валу генератора.
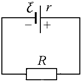Рис. 18.13
|
Прежде всего, заметим, что электрическая схема генератора с подключенной нагрузкой ничем не отличается от схемы, состоящей из батарейки, замкнутой на нагрузку с сопротивлением R (рис. 18.13). А для такой схемы ответы на все поставленные вопросы достаточно просты:
I = ℰ/(R + r); U = IR = [ℰ/(R + r)]×R или U = ℰ – Ir.
Полная мощность N = ℰI, полезная мощность
Р = UI = (ℰ – Ir)I. (18.2)
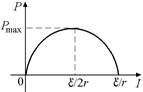Рис. 18.14
|
Из формулы (18.2) легко получим максимально возможное значение Р. Для этого проще всего построить график Р = Р(I) (рис. 18.14).
Как видим, максимальное значение достигается при токе I = ℰ/2r:
Рmax = [ℰ – (ℰ/2r)r]×( ℰ/2r) = ℰ2/4r. (18.3)
Бесполезная мощность (тепловые потери в якоре генератора) равна
Q = I2r. (18.4)
Вращающий момент, который необходимо приложить к валу генератора, чтобы обеспечить его вращение с циклической частотой w, найдем из следующих соображений.
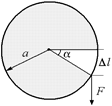Рис. 18.15
|
Если по касательной вала действует сила F, под действием которой вал радиуса а за время Dt поворачивается на угол Da (рис. 18.15), то сила F совершает работу
DА = FDl = FaDa.
Тогда мощность этой силы равна
.
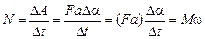Если пренебречь потерями на трение в генераторе, то именно такую полную электрическую мощность «производит» генератор:
Nэл = Nпол = ℰI = Мw Þ
М = ℰI/w. (18.5)
Чтобы привести генератор во вращение, необходимо затратить механическую мощность Nмех, при это генератор «произведет» электрическую мощность Nэл, только часть которой (Р) является полезной: Nэл = P + Q. Поэтому КПД генератора равен отношению полезной электрической мощности к затраченной:
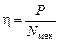. (18.6)
Задача 18.3. Какую ЭДС развивает динамо-машина постоянного тока, если при сопротивлении цепи R1 = 300 Ом на вращение машины затрачивается мощность N1 = 50 Вт, а потери на трение составляют a = 4,0 % от затраченной мощности. Какую мощность для поддержания того же числа оборотов необходимо затрачивать при сопротивлении цепи R2 = 60 Ом? Внутренним сопротивлением генератора пренебречь.
| R1 = 300 Ом N1 = 50 Вт a = 4,0 % R2 = 60 Ом r = 0 | Решение. Механическая мощность, затраченная на вращение генератора «расходуется» по двум каналам: 1) на производство электрической мощности Nэл =ℰI; 2) на потери, связанные с трением. Если N1 – заданная мощность, то aN1 – мощность потерь на трение. Тогда из закона сохранения энергии следует: N1 = ℰI + aN1 Þ N1 = ℰ2/R + aN1. (1) |
| ℰ = ? N2 = ? | |
Отсюда
ℰ =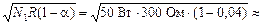 
120 В » 0,12 кВ.
По условию задачи при изменении нагрузки динамо-машины число оборотов поддерживается прежним. Поскольку ЭДС динамо-машины зависит только от скорости изменения магнитного потока, пронизывающего обмотку якоря, то при постоянном числе оборотов ЭДС индукции постоянна. На основании закона сохранения имеем
N2 = ℰ2/R2 + aN2. (2)
Преобразуем уравнения (1) и (2):
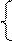 N1(1 – a) = ℰ2/R1
N2(1 – a) = ℰ2/R2
| 
|
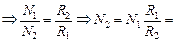
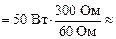250 Вт = 0,25 кВт.
Ответ: ℰ =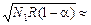 
0,12 кВ; 
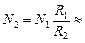0,25 кВт.
СТОП! Решите самостоятельно: В10, С2, С3, D1, D2.
Дата добавления: 2016-04-11; просмотров: 2428;