А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 3 страница
Запишем уравнения Парка-Горева в операторной форме:
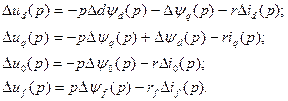 (3.91)
(3.91)
Для приращений потокосцеплений в операторной форме (в относительных единицах) можно записать
 (3.92)
(3.92)
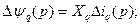 (3.93)
(3.93)
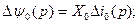 (3.94)
(3.94)
 (3.95)
(3.95)
Выражения 3.92)-(3.95) позволяют найти реактивности машины в операторной форме (под операторной реактивностью понимают отношение
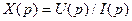 , где
, где 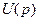 - падение напряжения в цепи;
- падение напряжения в цепи; 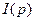 - ток в цепи).
- ток в цепи).
Известно, что в именованных единицах 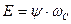 , следовательно, при переходе к относительным единицам получим
, следовательно, при переходе к относительным единицам получим 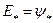 , так как
, так как 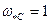 .
.
Тогда из (3.93) имеем
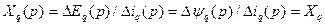 . (3.96)
. (3.96)
Аналогично из (3.94), получим
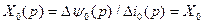 . (3.97)
. (3.97)
В продольной оси  расположены две обмотки: статора и ротора (учтем пока только обмотку возбуждения). Для определения
расположены две обмотки: статора и ротора (учтем пока только обмотку возбуждения). Для определения 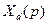 выполним преобразования:
выполним преобразования:
а) подставим выражение для 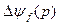 в выражение для
в выражение для 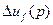 системы уравнений (3.91)
системы уравнений (3.91)
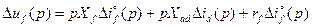 ,
,
откуда 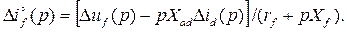 (3.98)
(3.98)
Далее, подставим выражение 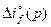 в (3.92)
в (3.92)
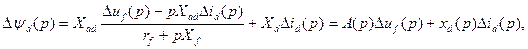 (3.99)
(3.99)
откуда 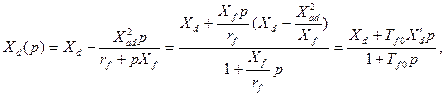 (3.100)
(3.100)
где 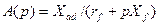 ;
;
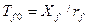 -постоянная времени обмотки возбуждения при разомкнутом статоре (в относительных единицах).
-постоянная времени обмотки возбуждения при разомкнутом статоре (в относительных единицах).
Заметим, что выражение для 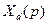 можно также получить из схемы замещения для
можно также получить из схемы замещения для 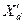 (рис.3.22), если в ветвь обмотки возбуждения дополнительно ввести активное сопротивление
(рис.3.22), если в ветвь обмотки возбуждения дополнительно ввести активное сопротивление 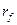 . В этом можно убедиться, если определить в операторной форме результирующее сопротивление схемы рис. 3.36.
. В этом можно убедиться, если определить в операторной форме результирующее сопротивление схемы рис. 3.36.
 Для машины с демпферными обмотками операторные реактивности можно получить из схем замещения рис.3.25 и 3.26, если их дополнить соответствующими активными сопротивлениями, как показано на рис.3.37, а и б.
Для машины с демпферными обмотками операторные реактивности можно получить из схем замещения рис.3.25 и 3.26, если их дополнить соответствующими активными сопротивлениями, как показано на рис.3.37, а и б.
 |
Рис.3.36.
Рис.3.37.
3.5. ВНЕЗАПНОЕ КОРОТКОЕ ЗАМЫКАНИЕ СИНХРОННОЙ МАШИНЫ
3.5.1.Внезапное короткое замыкание синхронной машины
без демпферных обмоток
Анализ электромагнитного переходного процесса при внезапном к.з. ограничим условием, что синхронная машина работает отдельно от других источников питания, а внешняя цепь ее статора при возникшем к.з. характеризуется неизменным постоянным сопротивлением, преимущественно индуктивным.
Рассмотрим вначале переходный процесс при отключенном устройстве автоматического регулирования возбуждения. Следовательно, 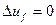 .
.
При металлическом трехфазном к.з. напряжение каждой фазы в месте к.з. равно нулю. Следовательно, приращение напряжения в этой точке при возникновении к.з. будет 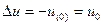 или в операторной форме
или в операторной форме 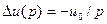 .
.
Тогда из (3.98) и (3.99) имеем:
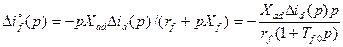 ; (3.101)
; (3.101)
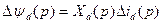 . (3.102)
. (3.102)
Далее, из (3.91) получим
 (3.103)
(3.103)
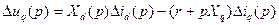 . (3.104)
. (3.104)
Решая совместно (3.103) и (3.104), найдем
 (3.105)
(3.105)
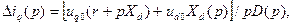 (3.106)
(3.106)
где определитель
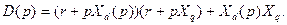 (3.107)
(3.107)
Далее, подставив в (3.107) выражение для 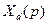 и, приравняв определитель нулю, получим характеристическое уравнение
и, приравняв определитель нулю, получим характеристическое уравнение
 (3.108)
(3.108)
Полученное уравнение является уравнением третьей степени относительно 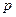 , аналитическое решение которого достаточно сложно.
, аналитическое решение которого достаточно сложно.
Для определения корней уравнения 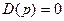 воспользуемся тем, что в условиях к.з. активные сопротивления цепи к.з. относительно малы по сравнению с ее индуктивными сопротивлениями.
воспользуемся тем, что в условиях к.з. активные сопротивления цепи к.з. относительно малы по сравнению с ее индуктивными сопротивлениями.
Тогда, полагая 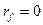 , получим
, получим
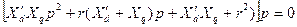 , (3.109)
, (3.109)
корни которого будут
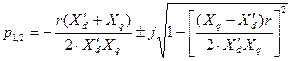 ;
; 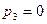 . (3.110)
. (3.110)
Первые два корня выражаются сопряженными комплексами и их действительная часть отрицательна, что указывает на затухание соответствующим им свободных токов с постоянной времени
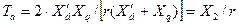 , (3.111)
, (3.111)
где 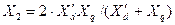 - представляет собой реактивность обратной последовательности машины.
- представляет собой реактивность обратной последовательности машины.
Найденные корни 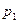 и
и 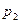 (при
(при 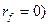 близки к действительности, а значение
близки к действительности, а значение 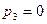 не соответствует физической сущности рассматриваемого процесса.
не соответствует физической сущности рассматриваемого процесса.
Уточним значение 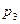 , положив
, положив 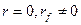 . При этом (3.108) переходит в уравнение
. При этом (3.108) переходит в уравнение
 (3.112)
(3.112)
корни которого будут:
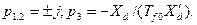
Таким образом, значение 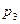 является вещественной отрицательной величиной, указывающей тем самым на то, что соответствующий
является вещественной отрицательной величиной, указывающей тем самым на то, что соответствующий 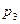 свободный ток затухает по экспоненте с постоянной времени
свободный ток затухает по экспоненте с постоянной времени
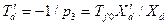 . (3.113)
. (3.113)
Зная корни уравнения (3.108), можно применяя формулу разложения [1] перейти от изображений (3.105)-(3.106) к временным функциям.
Для упрощения решения поставленной задачи введем еще дополнительное допущение, суть которого состоит в том, что при определении принужденных токов и начальных значений свободных токов примем 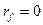 и
и 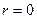 .
.
При этом затухание свободных токов ( то есть учет активных сопротивлений) будет отражено в значениях соответствующих постоянных времени затухания свободных токов.
Тогда выражения для 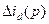 и
и 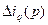 будут иметь вид:
будут иметь вид:
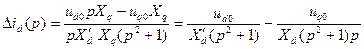 ; (3.114)
; (3.114)
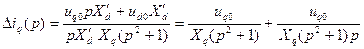 . (3.115)
. (3.115)
 |
По таблицам преобразования функций по Лапласу находим:
Поэтому оригиналами для выражений (3.114)-(3.115) будут
 ; (3.116)
; (3.116)

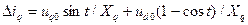 . (3.117)
. (3.117)
Прибавив к полученным приращениям токов их предшествующие значения 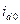 и
и 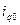 и приняв во внимание, что в соответствии с принятыми положительными направлениями осей
и приняв во внимание, что в соответствии с принятыми положительными направлениями осей 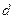 и
и 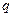 (см. рис.3.21)
(см. рис.3.21) 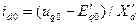 и
и 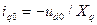 , получим
, получим
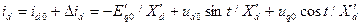 ; (3.118)
; (3.118)
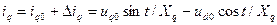 . (3.119)
. (3.119)
Далее, используя (3.81), можно перейти от переменных в осях  к переменным в фазных осях
к переменным в фазных осях 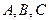 .
.
Так, например, для фазы 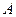 после преобразований получим: (3.120)
после преобразований получим: (3.120)
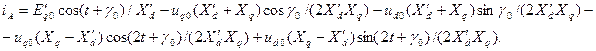
Полученное выражение не учитывает затухание свободных токов, для учета которого рассмотрим структуру (3.120).
Первый член (3.120) представляет собой периодическую слагающую тока основной частоты, амплитуда которой в момент времени 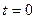 равна начальному переходному току. Эта слагающая вызвана э.д.с. вращения и ее изменение можно оценить, рассматривая отдельно действие этой э.д.с. при представлении машины операторной реактивностью
равна начальному переходному току. Эта слагающая вызвана э.д.с. вращения и ее изменение можно оценить, рассматривая отдельно действие этой э.д.с. при представлении машины операторной реактивностью 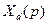 .
.
Тогда для приращения 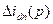 можно записать
можно записать
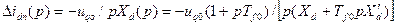 . (3.121)
. (3.121)
 |
Используя формулу разложения [1] , перейдем к оригиналу
Левая часть формулы разложения является функцией 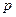 , правая часть – соответствующая ей функция времени
, правая часть – соответствующая ей функция времени 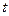 .
.
Далее, определим корни определителя 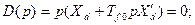
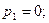
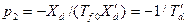
Тогда для 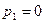 , имеем
, имеем 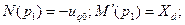 для
для 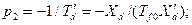
 .
.
Таким образом, можно записать
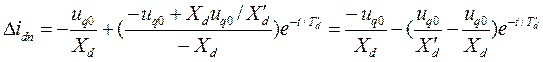 . (3.122)
. (3.122)
Прибавив предшествующий ток 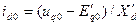 , после преобразований, получим
, после преобразований, получим
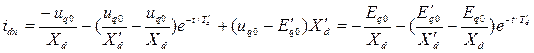 . (3.123)
. (3.123)
Полученная зависимость изменения тока  в координатах
в координатах 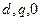 характеризует изменение огибающей кривой периодической слагающей тока статора основной частоты. Эта слагающая (при отсутствии поперечной демпферной обмотки в оси
характеризует изменение огибающей кривой периодической слагающей тока статора основной частоты. Эта слагающая (при отсутствии поперечной демпферной обмотки в оси 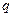 ротора и при неучете активных сопротилений цепи статора) является только продольной. Ее действующее (тепловое) значение в произвольный момент времени определяется выражением
ротора и при неучете активных сопротилений цепи статора) является только продольной. Ее действующее (тепловое) значение в произвольный момент времени определяется выражением
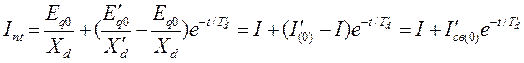 , (3.124)
, (3.124)
где 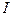 -действующее значение установившегося тока к.з.;
-действующее значение установившегося тока к.з.;
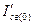 - действующее значение начального свободного переходного тока.
- действующее значение начального свободного переходного тока.
Для мгновенного значения периодической слагающей тока основной частоты фазы 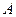 имеем
имеем
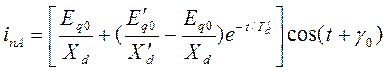 . (3.125)
. (3.125)
Остальные члены в (3.120) обусловлены действием трансформаторных э.д.с. и их затухание происходит с постоянной времени 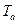 , определяемой выражением (3.111).
, определяемой выражением (3.111).
Таким образом, полное выражение для мгновенного значения тока фазы 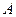 с учетом затухания свободных токов будет
с учетом затухания свободных токов будет
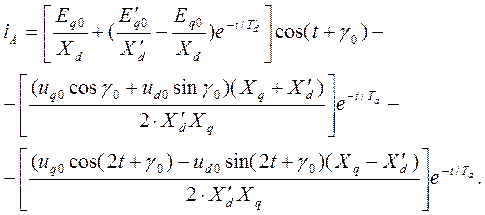 (3.126)
(3.126)
Здесь выражение в первых квадратных скобках образует периодическую слагающую тока основной частоты, вторая скобка – апериодическую слагающую и третья - вторую гармонику тока.
Все полученные выражения справедливы при к.з. как на выводах синхронной машины, так и в произвольной точке сети, присоединенной к машине.
В последнем случае, под 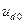 и
и  понимают составляющие предшествующего напряжения в точке к.з., а к каждой реактивности машины должна быть прибавлена внешняя реактивность до места к.з.
понимают составляющие предшествующего напряжения в точке к.з., а к каждой реактивности машины должна быть прибавлена внешняя реактивность до места к.з.
Аналогично, при определении 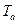 величина
величина 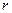 должна включать в себя активное сопротивление внешней цепи до точки к.з.
должна включать в себя активное сопротивление внешней цепи до точки к.з.
Определим теперь ток обмотки возбуждения.
Для компенсации магнитного потока, созданного током 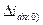 в обмотке возбуждения, возникнет свободный ток
в обмотке возбуждения, возникнет свободный ток 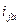 , начальное значение которого, приведенное к статору, определится из условия сохранения в начальный момент предшествующего потокосцепления обмотки возбуждения, то есть
, начальное значение которого, приведенное к статору, определится из условия сохранения в начальный момент предшествующего потокосцепления обмотки возбуждения, то есть
 ,
,
откуда 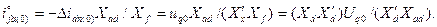
Очевидно, этот ток обмотки возбуждения будет затухать с постоянной времени 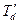 .
.
С другой стороны от апериодической слагающей тока статора в обмотке возбуждения будет наводится переменный ток синхронной частоты, зату-
хающий с постоянной времени 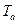 . Очевидно, что начальное значение этого тока должно быть равно
. Очевидно, что начальное значение этого тока должно быть равно 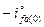 , чтобы в начальный момент к.з. в обмотке возбуждения сохранился предшествующий ток
, чтобы в начальный момент к.з. в обмотке возбуждения сохранился предшествующий ток 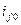 .
.
Следовательно, выражение для тока в обмотке возбуждения при внезапном к.з. в цепи статора будет:
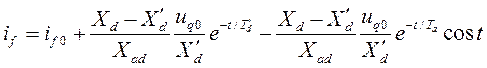 . (3.127)
. (3.127)
В качестве примера на рис.3.38 приведены кривые тока статора (в относительных единицах) синхронной машины при внезапном к.з, а на рис.3.39 приведены кривые изменения тока возбуждения (в относительных единицах) синхронной машины при внезапном к.з.
Графики построены при следующих параметрах генератора:
 МВА;
МВА; 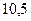 кВ;
кВ;  кА;
кА; 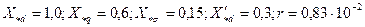 Ом;
Ом;
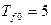 с; ток возбуждения холостого хода
с; ток возбуждения холостого хода 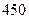 А. Генератор работает на холостом ходу с номинальным напряжением,
А. Генератор работает на холостом ходу с номинальным напряжением, 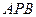 отключено.
отключено.
 |
Рис.3.38.
 |
Рис.3.39.
3.5.2.Влияние и приближенный учет демпферных обмоток
Общий путь исследования электромагнитного переходного процесса внезапного к.з. синхронной машины с демпферными обмотками принципиально тот же, что и в предыдущем параграфе.
Такая машина характеризуется операторными реактивностями в обеих
осях ротора. При этом каждая дополнительная обмотка на роторе будет повышать порядок определителя системы уравнений, аналогичной (3.105)-(3.106). Так, если по осям 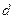 и
и 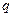 будет расположено по одной демпферной обмотке, то показатель степени
будет расположено по одной демпферной обмотке, то показатель степени 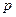 в определителе будет равным пяти.
в определителе будет равным пяти.
При этом решение характеристического уравнения, получающегося путем приравнивания определителя нулю, в общем виде невозможно.
Близкое к действительности решение можно получить, если пренебречь активными сопротивлениями ротора и статора.
При таком подходе корни характеристического уравнения 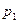 и
и 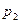 могут быть определены по (3.110), где вместо
могут быть определены по (3.110), где вместо 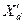 и
и 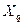 нужно ввести соответственно
нужно ввести соответственно 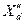 и
и 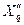 . Для определения значений
. Для определения значений 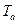 и
и 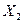 должна быть сделана аналогичная замена в (3.111).
должна быть сделана аналогичная замена в (3.111).
Остальные корни находят, предполагая активное сопротивление цепи статора равным нулю ( 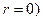 .
.
В продольной оси, где расположены две обмотки ротора (возбуждения и демпферная), переходный процесс характеризуется постоянными времени 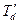 и
и 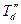 , которые обратны по величине соответствующим корням и противоположны им по знаку, то есть
, которые обратны по величине соответствующим корням и противоположны им по знаку, то есть 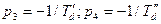 .
.
В поперечной оси переходный процесс характеризуется постоянной времени 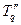 , которая обратна по величине и противоположна по знаку корню
, которая обратна по величине и противоположна по знаку корню 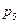 (на роторе расположена только одна демпферная обмотка).
(на роторе расположена только одна демпферная обмотка).
В соответствии с (3.77) для периодической слагающей тока фазы 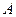 можно
можно
записать 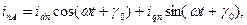 (3.128)
(3.128)
где  и
и 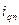 определяются из выражений
определяются из выражений
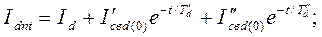 (3.129)
(3.129)
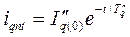 . (3.130)
. (3.130)
Полное выражение для мгновенного значения тока фазы 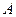 по аналогии с (3.126) имеет вид
по аналогии с (3.126) имеет вид
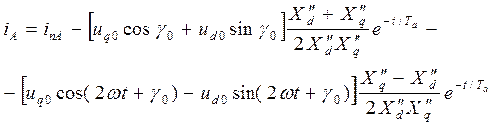 . (3.131)
. (3.131)
3.5.3. Влияние автоматического регулирования возбуждения
при внезапном коротком замыкании
Под устройством автоматического регулирования возбуждения условимся понимать в рассматриваемом случае простейшее устройство релейной форсировки возбуждения, которое приходит в действие при соответствующем снижении напряжения генератора (рис.3.40).

Рис.3.40.
а- принципиальная схема;
б – основные характеристики;
в –кривая нарастания напряжения 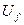 во времени
во времени
Рассмотрим процесс форсировки возбуждения синхронной машины, имеющей электромашинную систему возбуждения при работе возбудителя по схеме самовозбуждения.
При снижении напряжения за установленный уровень реле напряжения 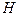 замыкает цепь контактора
замыкает цепь контактора 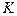 , который в свою очередь закорачивает реостат цепи возбуждения.
, который в свою очередь закорачивает реостат цепи возбуждения.
Пренебрегая относительно малым сопротивлением якоря, характеристику холостого хода (х.х.х.) возбудителя можно считать также его нагрузочной характеристикой. При этом рабочее состояние возбудителя с самовозбуждением определяется точкой пересечения х.х.х. с прямой, соответствующей уравнению 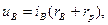 где
где 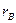 и
и 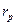 -омические сопротивления обмотки возбуждения возбудителя и реостата цепи возбуждения возбудителя, соответственно(рис.3.40, a).
-омические сопротивления обмотки возбуждения возбудителя и реостата цепи возбуждения возбудителя, соответственно(рис.3.40, a).
При закороченном реостате новое установившееся состояние возбудителя определяется пересечением той же характеристики с более пологой прямой
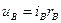 , от положения которой зависит предельное напряжение возбудителя
, от положения которой зависит предельное напряжение возбудителя 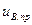 (см.рис.3.40, б).
(см.рис.3.40, б).
Разность ординат х.х.х. и прямой 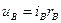 представляет для каждого значения тока
представляет для каждого значения тока 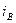 напряжение, уравновешивающее э.д.с. самоиндукции обмотки возбуждения возбудителя, которая возникает при переходе тока
напряжение, уравновешивающее э.д.с. самоиндукции обмотки возбуждения возбудителя, которая возникает при переходе тока 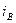 от своего предшествующего значения к предельному.
от своего предшествующего значения к предельному.
Получающаяся при этом закономерность нарастания напряжения возбудителя имеет сложный характер.
В первом приближении, эту сложную закономерность (сплошная кривая на рис.3.40, в) заменяют экспонентой с постоянной времени 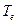 (пунктирная кривая на том же рисунке), считая практически при этом
(пунктирная кривая на том же рисунке), считая практически при этом 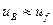 , то есть
, то есть
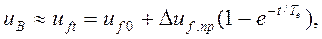 (3.132)
(3.132)
где 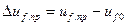 - предельное приращение напряжения на кольцах обмотки возбуждения синхронной машины.
- предельное приращение напряжения на кольцах обмотки возбуждения синхронной машины.
Величина 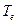 обычно находится в пределах
обычно находится в пределах 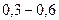 с.
с.
Выражение для временной зависимости изменения тока возбуждения при условии, что машина не имеет демпферных обмоток и ее цепь статора замкнута на внешнюю реактивность 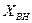 имеет вид
имеет вид
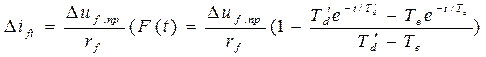 . (3.133)
. (3.133)
Продолжительность подъема напряжения машины под действием форсировки возбуждения до нормального значения называют критическим временем  .
.
При этом будем считать, что переходный процесс практически заканчивается как только восстановлено напряжение генератора, то есть при наличии 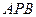 продожительность переходного процесса равна
продожительность переходного процесса равна  .
.
В начальный момент к.з., в силу инерции магнитных потоков, сцепленных с обмотками, влияние 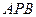 отсутствует. В дальнейшем действие
отсутствует. В дальнейшем действие 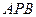 сказывается в росте тока возбуждения и связанных с ним составляющих тока статора и продольной демпферной обмотки.
сказывается в росте тока возбуждения и связанных с ним составляющих тока статора и продольной демпферной обмотки.
Апериодическая слагающая и связанная с ним вторая гармоника тока статора остаются такими же, что и при отсутствии 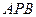 , что позволяет их не учитывать.
, что позволяет их не учитывать.
Рассмотрим простейший случай, когда к обмотке возбуждения генератора без демпферных обмоток в момент к.з. подводится сразу предельное напряжение 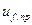 , что соответствует
, что соответствует 
Дата добавления: 2016-04-14; просмотров: 1448;
